Оглавление:




Определение напряжений в стенках сосудов по безмоментной теории
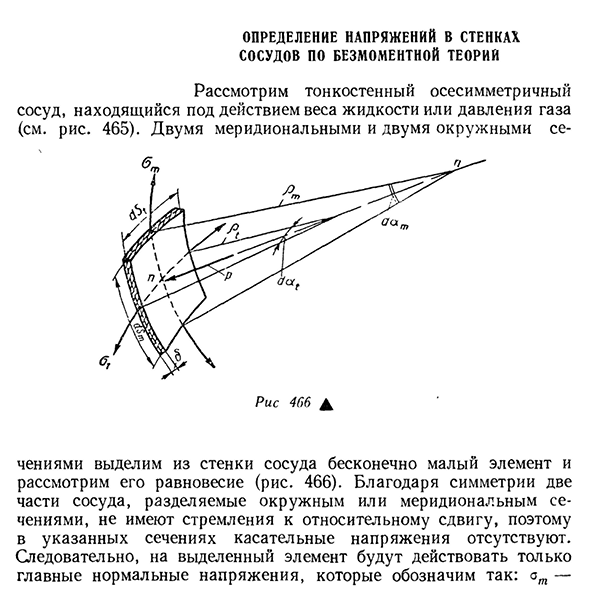
- Определение напряжения стенки Работы по теории БЕЗМ0МЕНТН0Ы Рассмотрим тонкостенный осесимметричный сосуд под весом жидкости или давлением газа(см. рисунок). 465). Двумя меридиональными и двумя окружностями СЕ Отделим бесконечно
малые элементы от стенок сосуда и рассмотрим его равновесие(рис. 466). Из-за симметрии две половины сосуда, разделенные кольцевой секцией или секцией направления Север-Юг, не наклонены относительно сдвига, эти секции не симметричны.
Итак, на выбранный элемент действует только основное нормальное Людмила Фирмаль
напряжение. — 559 меридиональное напряжение (оно действует на участке Окружного сечения) и-окружное напряжение. Согласно теории импульса, напряжение области и площади плоскости элемента предполагается равномерно распределенным. Кроме того, все размеры контейнера обусловлены промежуточной поверхностью его стенок. Средняя поверхность сосуда представляет собой поверхность двойной кривизны. Радиус кривизны меридиана в
рассматриваемой точки обозначают буквой ПТ, а другой радиус кривизны сегмента 465, б) нормальной поверхности, заключенной между рассматриваемой точки срединной поверхности и осью 0-0), который представляет его: силу<ЗТ на плоскость элемента, а на внутренней поверхности выделенного элемента, Давайте спроецируем данную силу на нормальное p-p: Здесь на диаграмме
- записан первый член. 467 для обозначения проекции элементов на меридиональную плоскость. Второй член написан по аналогии. Замените знак b (a) аргументом из-за малости угла и замените все на Y8 {(18T、 Или дано < ^ Т1. / У<1А/Р^8Т-г(1$1 0 L h1AA t1(1Z (91) WZT?т+__■год • 9Т Р/О , Наконец найти (19.1) 560 соотношений (19.1) называется уравнением Лапласа, которое получило его в начале прошлого века при изучении поверхностного натяжения в жидкостях. Здесь уместно отметить аналогию тонкой пленки
жидкости с поверхностным натяжением со стенкой сосуда. Например, и пленка, и стенки сосуда, испытывая напряжение, должны удерживать в равновесии определенный объем жидкости с поверхностью определенной формы. Поэтому капли, лежащие на неводной поверхности, не будут распространяться только за счет силы поверхностного натяжения.
Отметим, что данный пример имеет много преимуществ в сравнении, подсказывая конструктору каплевидные резервуары, используемые для хранения Людмила Фирмаль
нефтепродуктов Ние 468A Другие резервуары (рис. 468). Это уравнение содержит два неизвестных напряжения, a(и ZT). Но напряжение at можно определить из другого уравнения, а затем посмотреть на общую проекцию на ось O-o силы, действующей на отсечный объем сосуда, используя уравнение Лапласа 465, b). Площадь окружного сечения стенки сосуда равна формуле 2тс / ^O.It можно рассчитать по формуле: И так оно и есть., Из 2 попс а-р ТС в ця7?2-Ф=О, Откуда О Р/? Т2 6 поп < 2 2ТЭ р о поп*(19.2) Здесь С2-жидкость, лежащая под весом и окружным сечением сосуда; р-согласно закону Паскаля, давление в жидкости одинаково во всех направлениях и равно UI.、 В некоторых случаях жидкость может храниться в контейнере с определенным
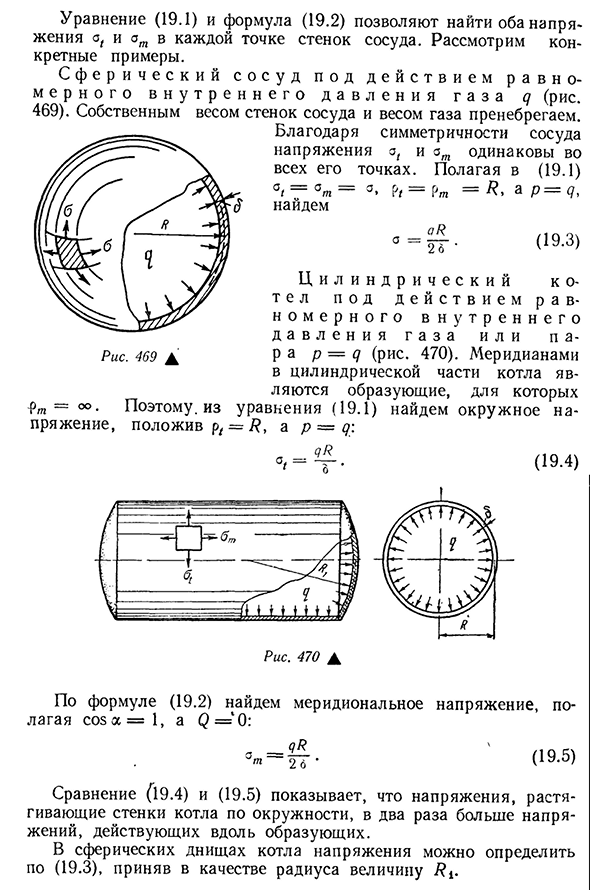
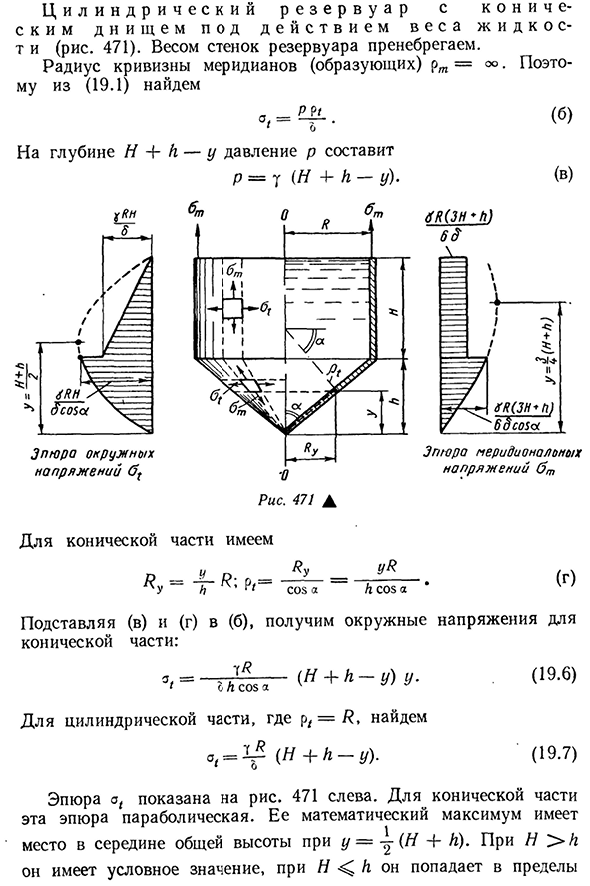
количеством избытка по сравнению с атмосферным давлением<7. В этом случае p=y K+ 561 уравнение (19.1) и уравнение (19.2), мы можем найти как напряжение, так и в каждой точке стенки сосуда. Давайте возьмем конкретный пример. Вы можете предоставить услугу, предоставив услугу.вы можете предоставить n услуг.469), которые могут предоставлять n услуг. Мертвый груз стенок сосуда и вес газа мы игнорируем. Благодаря симметрии сосуда, напряжения o ии он имеет условное значение,в N он входит 563коническая часть и имеют действительное значение, равное Один. Тер = -7/?(Н4-ы) 2 5 и поп а (19.8) Перейдем к определению меридионального напряжения. Для конической части находим объемный жидкий вес конуса высотой Y.: p1P2 7=71U3#2U Ku=-1- — — (/d)\подставляя(V), (g) и (d) в(19.2), получаем
%=- [3 (y+L)-2</]y.(19.9) график at показан на рисунке. Максимум участка, который также очерчен о конической части 471 параболой справа, становится z с y=—(N+/g). Действительное значение имеет только/ / <1^ — / g, когда оно находится в пределах конической части и равно следующему значению Tah o t=~16O CO5a в цилиндрической части напряжение от высоты o постоянное и равно напряжению на верхнем конце в месте подвеса бака: а у? (ZN4-L) на 65 (19.10)) (19.11) Места, где поверхность сосуда имеет резкий излом, например, цилиндрические и конформные соединения(рис. 471), или сферическая радиальная часть меридианного напряжения, как
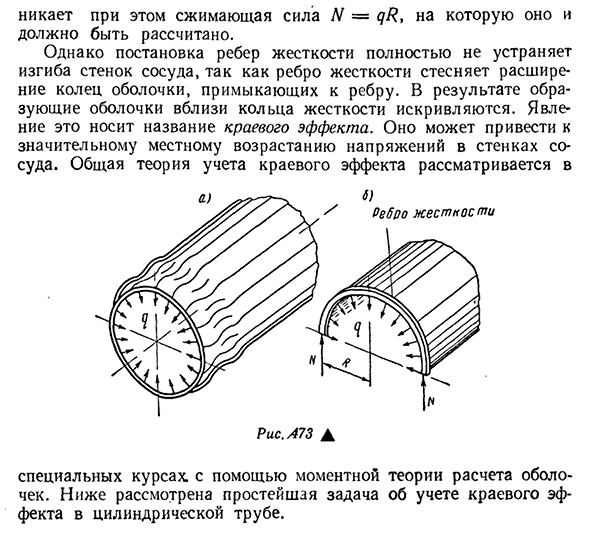
показано, находится в равновесии В У сетевого расположения(рис. 470) детали, l=<не ZT81pa на рисунке. Эта составляющая по периметру кольца 472 создает радиальную нагрузку<7 = Bat81pa, которая стремится загнуть края цилиндрической оболочки внутрь(фиг. 473, а). Чтобы устранить этот изгиб, ребра жесткости расположены в виде углов или каналов, которые окружают сосуд в месте перелома. Как показано на рисунке, эта кромка принимает радиальную нагрузку<7. 473,6 Из равновесного состояния полукруга, полученного при разрезании ребра жесткости по диаметру, ребро является- Существует
ли сила сжатия 564 AG=d/?А для этого нужно все просчитать. Однако установка арматуры не полностью устраняет изгиб стенки сосуда, так как ребра жесткости ограничивают расширение кольца оболочки, прилегающего к кромке. В результате формованная оболочка вблизи жесткого кольца изгибается. Это явление называется краевым эффектом. Это может привести к значительному локальному повышению давления на стенку сосуда. Общая теория учета краевых эффектов является、 R есть./ 173А Специальный курс, использующий теорию моментов расчета оболочки. Рассмотрим краевой эффект цилиндрической трубы простейшими задачами являются:
Смотрите также:
| Расчет на прочность при переменных напряжениях | Краевой эффект в цилиндрической оболочке |
| Понятие о безмоментной и моментной теориях расчета сосудов | Чистый изгиб. определение нормальных напряжений |

