Оглавление:
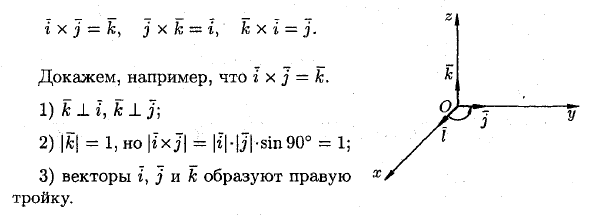

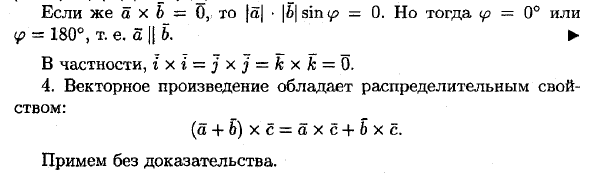
Векторное произведение векторов и его свойства
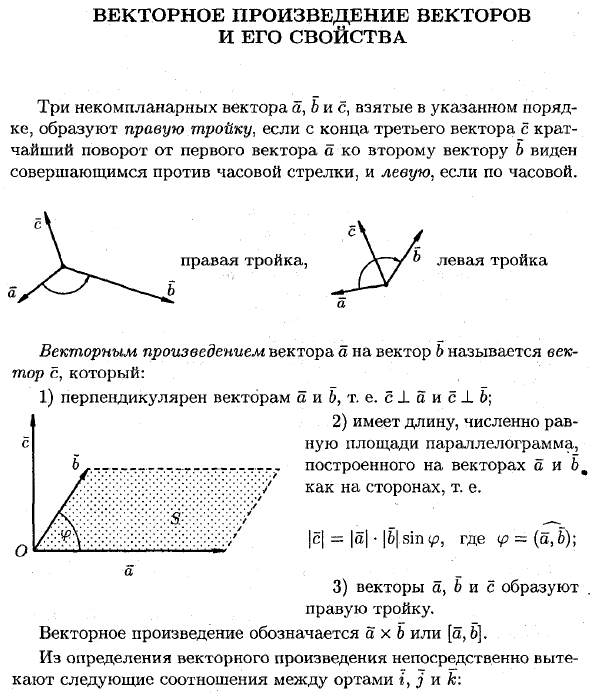
- Векторные произведения и их характеристики Если кратчайший поворот от конца третьего вектора к первому вектору a ко второму вектору b происходит против часовой стрелки и по часовой стрелке слева, три несоответствия выполняются в указанном порядке Векторы граней a, b и c образуют правильную тройку.
c. 1) перпендикулярно вектору o, т.е. i o и c ± b; 2) имеет длину, численно равную площади параллелограмма, построенного на векторах а и 6. б левый 3 но | И | = \ О. \ • \ b \ sin <pi, где ip = (a, 6); 3) Векторы a, 6 и c образуют правильную тройку. Векторное произведение обозначено как a x b или [a, 6]. Следующее соотношение между единичными векторами r, j, k следует непосредственно из определения векторного произведения.
Право 3 но Векторное произведение вектора a и вектора b на вектор Людмила Фирмаль
g x j = fc, j x k = g, k x g = j Например, давайте докажем, что r x j = ic. 1) от 1 до 1 2) | fc | = 1, но | »TxJ | = | i | * | J | * sin 90 ° = 1; 3) Векторы r, j, k образуют правую тройку.Свойства векторного продукта 1. Перестановка факторов меняет знак векторного произведения. То есть a x 6 = — (6 x a). << Векторы для xb и bxa коллинеарны и имеют одинаковый модуль (площадь параллелограмма не изменяется), но в противоположном направлении (a, 6, a 6 и a, 6, bxa перевернута). Следовательно, 5×5 = = — (6 x a). ► 2.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Векторное произведение имеет характеристику связи по скалярным коэффициентам. То есть A (a x b) = (Aa) x 5 = a x (AS). А> 0. Вектор A (a x 6) перпендикулярен векторам a и b. Вектор (Aa) x b также перпендикулярен векторам a и b (векторы a и A a находятся в одной плоскости). Таким образом, векторы A (a x 6) и (Aa) x b коллинеарны. Очевидно, что их направления последовательны. Они имеют одинаковую длину: A (a x 6) | = A | a x b \ = A | a | -16 | • Грех (S, 6) И ^ | (Aa) x 6 | = | Aa | • | 6 | -син (Aa, 5) = A | a |. | 5 | грех (а, с). Следовательно, A (a x 6) = Aa x b.
То же самое можно сделать для A <0. ► 3. Два ненулевых вектора a и 6 коллинеарны, только если их произведение равно нулевому вектору, то есть a ||. B <=> 5×6 = 0. • 4 || 6, угол между ними 0 ° или 180 °. Но тогда | a x 6 | = \ a \ • | b | • sin (a, b) = 0. Так что axb равен 0. AXB о Bas Если a x b = 0, | a | • | 6 | sin ip = 0. Но ip = 0 ° или H> = 180 °, то есть 51 | 5.► В частности, ixi-jxj-khk = 0. 4. Векторные продукты имеют свойства распространения. (A + D) хс = ахс + 6хс.
Принять без доказательств. Людмила Фирмаль

