Оглавление:





Вынужденные колебания упругой системы
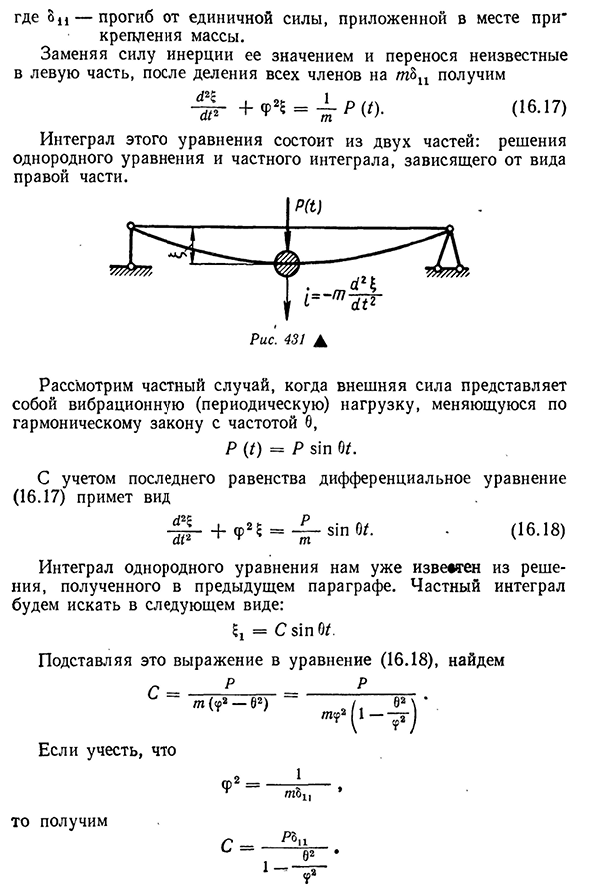
- Вынужденные колебания упругой системы Если на систему воздействует сила р ( / ), если она изменяется во времени по произвольным законам, то колебания балки, вызванные действием этой силы, называют вынужденными, после приложения
инерционной силы балку в состоянии отклонения можно считать находящейся в равновесии фиг. 431). Упражнение 5 теперь должно определяться из двух сил: I и P(/): 5=8и [>+ / >(/)], 518gde — » отклонение от единицы силы, приложенной при фиксации массы.
Замените силу инерции на ее величину и переместите неизвестную часть влево, предварительно разделив все члены на+OO). С учетом затухания Людмила Фирмаль
(внутреннего сопротивления) вместо уравнения (16.17) получаем следующее дифференциальное уравнение: 520j+2º. +h=4 8!P « (16.21) формула вынужденных колебаний (16.21) отличается от формулы собственных колебаний (16.13) только наличием правой части, но коэффициенты в первой производной- & •вместо Формулы (2 16.13)
формула (16.12) может быть использована с условием, что значение x не является постоянным и зависит от частоты результаты теории и опыта более последовательны, предполагая, что в собственных колебаниях x= = = b-2G^ «‘ A In и W и x s I происходят колебания с частотой 6, x=XE•. (Где 7-логарифмический декремент распада.)Этим объясняется тот факт, что коэффициенты 2^и 2^(16.13) и (16.21)
- различны с учетом эффекта сопротивления. Соотношение двух коэффициентов-y-выглядит так- Девять Решение —- : (16.22) Частичное решение уравнения (16.21), которое соответствует чисто вынужденному колебанию, может быть записано как:&=81p6/+B2POPs6/. (16.23) если вы присвоите это выражение выражению (16.21) и объедините термины, содержащие 51p0/и sob/, вы получите (F2-92)^-2^51P 9/ 4- [2^10^1 -|-(CP2-92) B21 соз 6/=0. Это
уравнение должно быть погашено одинаково с любым значением/. Это условие выполняется, когда коэффициенты zco/и POPs6 / равны нулю. В результате получаем два неизвестных 5 4 и 5 2 и два уравнения: (F2_B2)B,-2π, 9vg= 4 ; 2 ^ 6 ^ 4- (F2-92) B2=0. K214 (16.24) Когда мы решаем уравнение, мы получаем、 — е а ) В= _ _ ___• (? 2 _ 0 2 )2 | 4^202 > П ~ » (^ 2 — 02)2 4^202 « Кроме того, формула для вынужденной вибрации (16.23) удобно выражается следующим образом $ = = В 31 и(6/+V!да что с тобой такое? (16.25) где B и V! — Амплитуда и фаза вынужденных колебаний; Если мы рассмотрим его на 81P(0/ 4- *4)=81P при 6 / SO8SO8 6 / 81P V!, Легко установить связь между константами 2 и in, U4: B1=SO8 U1;in 2=5z1p U4. Квадрат левой и правой частей этих уравнений и сложить их, мы находим Б2=Б? + Б1, И правильные части друг к другу. 71VG * наконец-то Но после раскола налево
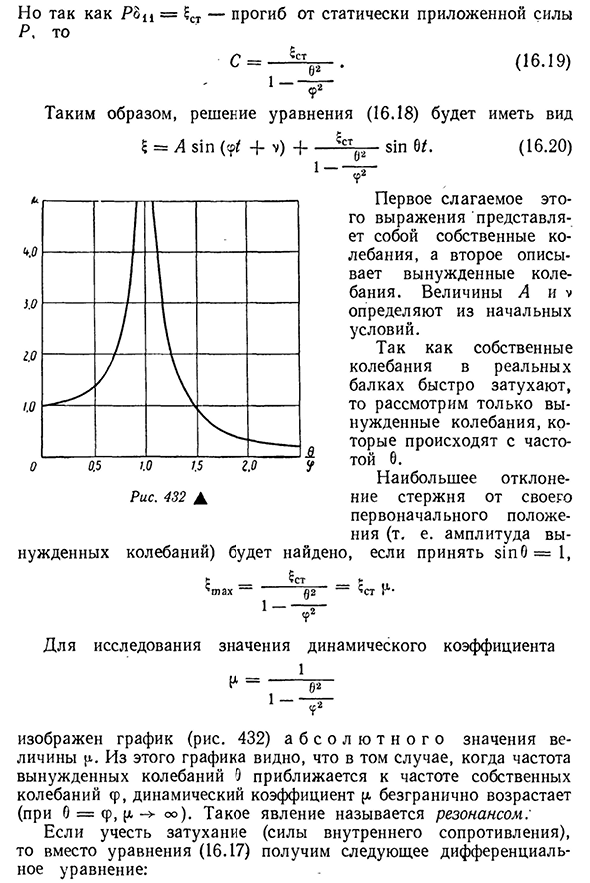
Принять во внимание равенство(16.24), В=+ * * У нас есть П_ Тонны И B=Z G S^0 2^2 • С тех пор — =- ^—А — С2^ Т?ул* Это In=^St, где динамический Людмила Фирмаль
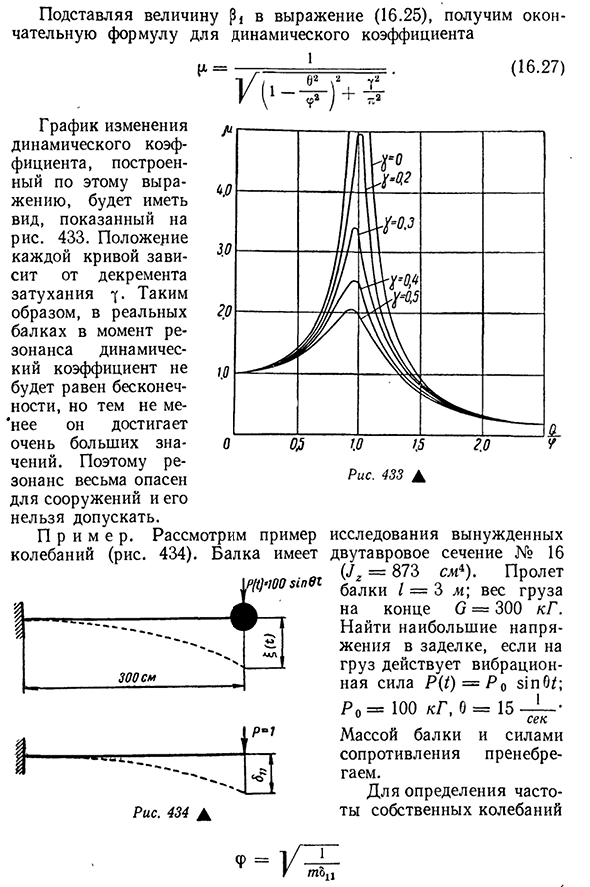
коэффициент[l определяется уравнением Р2 1 И1= -……. — . …….- =- *MB26) /(? 2 _ 02)2 + 4^ 202 . В 2\2. LO2B2g И1 -? ) Используя равенство(16.22) и (16.16)、 Подставляя значение уравнения 522 (16.25), получаем конечное выражение динамического коэффициента (16.27) График изменения динамических коэффициентов, построенный по этой формуле, имеет вид, показанный на рисунке. 433 положение каждой кривой зависит от демпфирования 7. Таким образом, в реальном пучке момента резонанса динамический коэффициент не равен бесконечности, но все же достигает очень большого значения. Поэтому резонанс очень опасен для структуры и не должен допускаться. П р и М Е Р. Рассмотрим пример исследования
вынужденных колебаний(рис. 434). Балка имеет сечение I балки № 16 og 0 г=873 см). Пролет I = = 3 м; вес груза Но Икс/ * — ** 300см Арас. Г Рис 434А В конце С=300 кг. Если нагрузка является колебательной силой P (1)=P0zsho/;то найти максимальное напряжение в уплотнении.P o=U0kg, 6=15—’ Считанные секунды Масса балки и сила ее сопротивления игнорируются. Определить частоту собственных колебаний 523находим массу Тонны — Шесть. Восемь. Триста. Девятьсот восемьдесят один =0,306 кг * сек2см И отклонение конца
луча от силы блока /3_zoo3 11-ZE / «3 * 2.1 * 10E * 873 =0,0049 см. Присвоить значение t и дать ему Один. 0,306-0,0049 25.83 Один. Считанные секунды • Динамический коэффициент равен следующим значениям Один. Момент в заделке будет мигать=300-300+100-300-1, 51=135 300 кг-см. Вычислить момент сопротивления нет. =- /~=109cm3dim максимальное напряжение Нахо Отчет Сто девять М135 300 1241кг / см?
Смотрите также:

