Проекция вектора на ось

Проекция вектора на ось

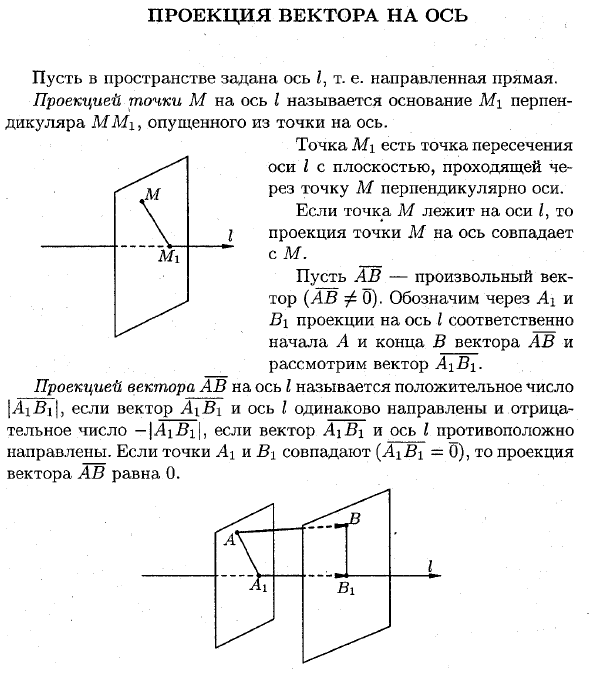
• Векторная проекция на ось Ось / задается пробелом, то есть направленной линией. Проекция точки M на ось I является основанием M \ вертикали MMx и не указывается в точке на оси. Точка Mi является пересечением оси I и плоскости, которая проходит через точку M перпендикулярно оси. Если точка M находится на / на оси, проекция точки M на ось совпадает с M.

Пусть AB произвольный вектор (ABφ0). Обозначим через Ai и B \ проекции на ось I начала и конца A в векторе AB соответственно и рассмотрим вектор A \ B . Проекция вектора AB на ось I является положительным числом \ AiB \ Вектор A \ B \ имеет то же направление, что и ось I, отрицательное число | i4i # i | Когда вектор A \ B \ имеет противоположное направление относительно оси I, точка A \ и B \ совпадают (A \ _B \ = 0), проекция вектора AB равна 0.

Пусть AB произвольный вектор (ABφ0). Обозначим через Ai и B \ проекции на ось I начала и конца A в векторе AB соответственно и рассмотрим вектор A \ B . Людмила Фирмаль

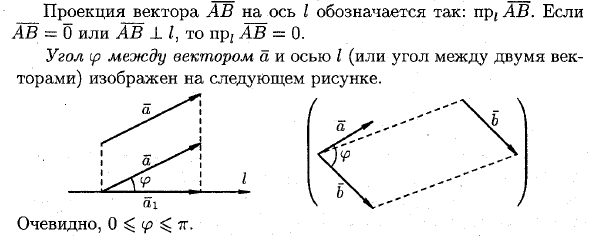
Проекция вектора AB на ось I выражается как npzAB. Pr, AB = 0, когда AB = 0 или AB ± 1. Угол ip между вектором а и осью I (или угол между двумя столетиями) Очевидно, 0 $ (p ^ 7Γ. Давайте рассмотрим некоторые основные характеристики проекции. Свойство 13.1 Проекция вектора a на ось I является произведением модуля вектора a и косинуса угла
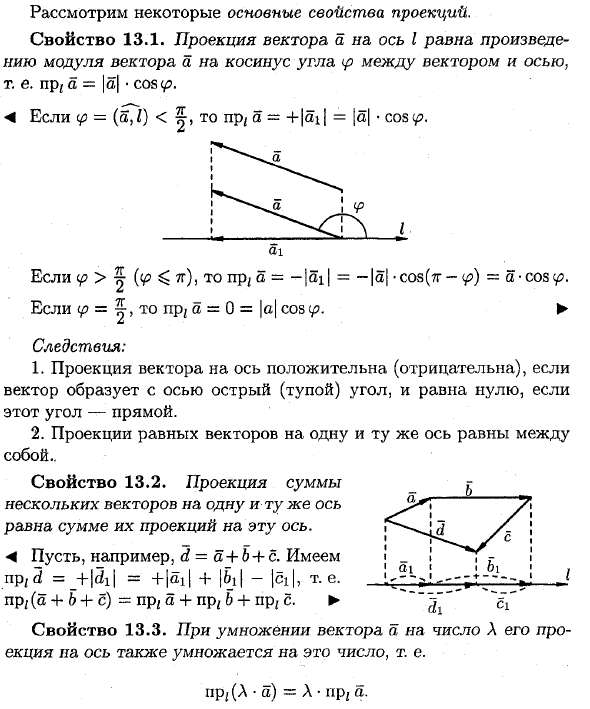
^ ((p ^ 7r), pr / a = — | 3i | = ~ | a | -cos (i * -4?) -a-cos (с. Если <p = ~, pr / o = 0 = \ a \ cos

• Решение задач по высшей математике

Системы линейных однородных уравнений	Разложение вектора по ортам координатных осей. Модуль вектора направляющие косинусы
Векторы и линейные операции над ними	Действия над векторами, заданными проекциями

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• ► Результат: 1. Проекция вектора на ось является положительной (отрицательной), если вектор образует острый угол (тупой угол) с осью, и нулевой, если этот угол является прямой линией. 2. Проекция равных векторов на одну и ту же ось равна друг другу. Свойство 13.2. Проекция суммы нескольких векторов на одну ось равна сумме проекций на эту ось. <Например, d = a + 6 + c. pr / 5 = _ + | 5i | = + \ ai \ + | 6i | — | ci |, т.е. prDa-b S + c) = pr, и 4-pr / 6 + pr, s ►Cl Свойство 13.3.

■ Если 4Λ> 0, npj (A-a) = | La | -cos y? = L- \ a \ -cosy? = L • pr / a. (Недвижимость 1) Если A <0: pr {(A • a) = | La | • cos (7r-ip) = -L • | a | • (-cos ^) = = L • a • cos v? = A • pr (a. Если A = 0, это свойство явно верно. ► Таким образом, линейные операции на векторах приводят к соответствующим линейным операциям на проекции этих векторов.

Умножение вектора a на число A также умножит это число на проекцию оси. npj (A • a) = Л • npz a. Людмила Фирмаль