Оглавление:



Собственные колебания системы с одной степенью свободы
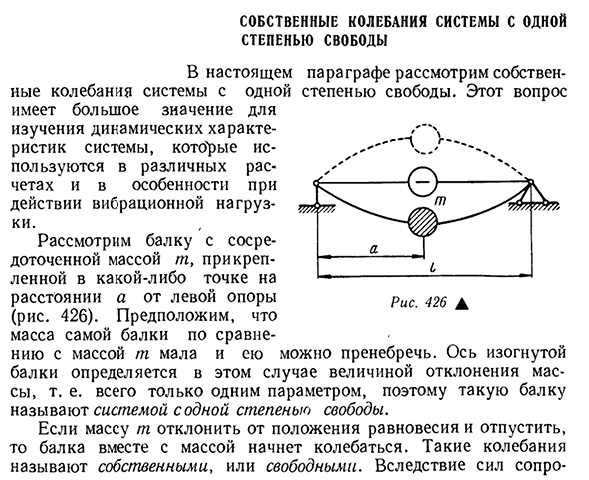
- Система естественной вибрации Степень свободы В этом параграфе рассмотрим степени свободы. Эта задача при исследовании колебаний одной системы очень важна для изучения динамических свойств систем, используемых в различных расчетах, особенно при действии колебательных нагрузок. Рассмотрим балку с
сосредоточенной массой t в точке, находящейся на расстоянии a от левой опоры(рис. 426). Предположим, что масса самого пучка меньше массы т и пренебрежимо мала. Поскольку ось криволинейного пучка определяется в данном случае величиной отклонения массы, то есть только одним параметром, такой пучок может иметь
определенную степень свободы. Когда масса т отклоняется от положения равновесия Людмила Фирмаль
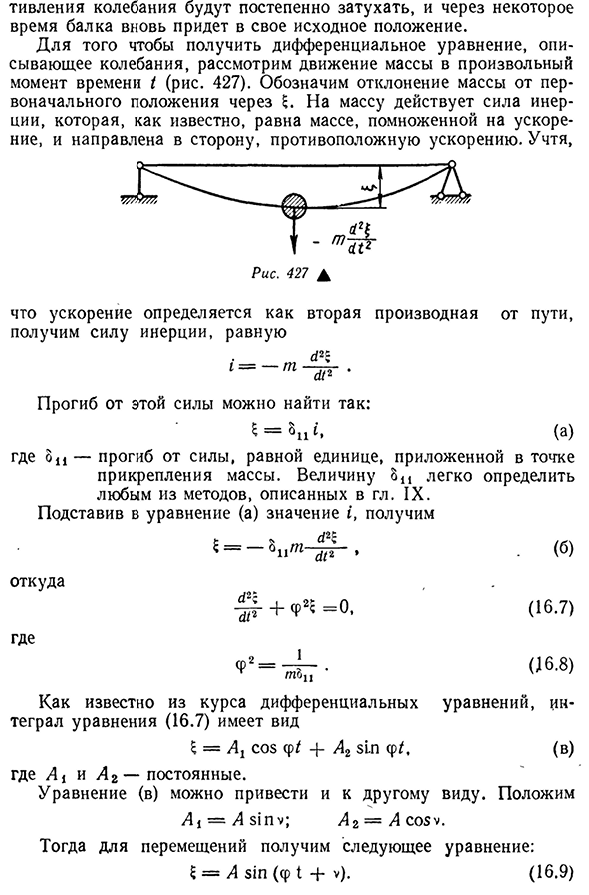
и освобождается, пучок начинает колебаться вместе с массой. Такие колебания называются их собственными, или свободой. В результате силы сопротивления- 17 заказ № 1037 513 вибрация постепенно исчезнет, и через некоторое время Балка вернется в исходное положение. Рассмотрим движение массы в любой момент времени для получения дифференциального уравнения, описывающего
колебания/(рис. 427). Известно, что она равна массогабаритным силам инерции, указывающим на отклонение массы от исходного положения. Считать, Что ускорение определяется как квадратичная производная пути, то получим силу инерции, равную Отклонение от этой силы можно найти следующим образом:=(а) здесь отклонение от силы равно силе, приложенной в точке крепления массы. Это значение легко определяется любым из методов, описанных в главе
- IX. Если вы присвоите значение I выражению (a), то получите:= — ^11SH___, (b) Откуда Куда? +Ф2^=0,(16.7) (16.8) Как известно из курса дифференциальных уравнений, Интеграл уравнения (16.7)равен B=CP/4-L2z1p f/, где (b) A{и A2-константы. Выражение (b) может быть сведено к другой форме. Поставим D 1=L81pu; a2-C. 08u. Тогда для смещения получим следующую формулу: 5=A81P (f I4-y). (16.9 )) Для
скорости движения массы 514 существуют две константы A и V, которые определяются из первого условия уравнения (f/4-V) (16.10) V-=A f Sov (16.9) и (16.10). Пусть для I=0 Тогда из уравнений (16.9) и (16.10) А 81P=?В ; Поп-ф В= = 1/0. И если вы решите эти уравнения График изменения во времени показан на рисунке. 428. Максимальное отклонение в ту или иную сторону будет иметь место, когда 81p (f/-N) принимает одно значение.
Как видно из уравнения (16.9), оно будет равно константе А. время, когда создается полный цикл колебаний, называется периодом колебаний. Каждые T секунд отклонение 5 Людмила Фирмаль
получает старое значение. Из уравнения (16.9), 5=a81p (f/4-V)==a81p[f (/4-T) 4-таким образом, F T=2K, Семнадцать.* 515, число колебаний в 2tg секундах равно Ф.- = Согласно формуле обозначения (16.8) имеем С 6-1′) По формуле (16.11) определяется теоретическое значение круговой частоты собственных колебаний системы определенной степени свободы(частота 2тсек). Если масса t зафиксирована в середине пролета второй опорной балки, то отклонение от
единичной силы, как известно, определяется уравнением. 811=48^7′ Для этой задачи 1 / 48E/ Уравнение показывает, что частота колебаний возрастает с увеличением жесткости балки и уменьшается с увеличением пролета. Она также обратно пропорциональна массе Т. Если к балке присоединена некоторая масса(например, n), то система имеет n степеней свободы. В этом случае система имеет несколько собственных частот. Приведенные выше решения являются приблизительными, так как в них не учитываются силы сопротивления: сопротивление воздуха, сила трения на стыках, внутреннее сопротивление и др. Сила аэродинамического
сопротивления в колебательной скорости, наблюдаемой в пучке, незначительна, так как она мала. Сила трения соединения может быть устранена или сведена к минимуму путем улучшения конструкции шарнирной опоры или смазки. Основной силой является внутреннее неупругое сопротивление, которое зависит от материала балки и многих других факторов. Эти силы не могут быть устранены. Согласно одной из наиболее распространенных гипотез учета затухания,предложенной Фойгтом,балочный материал рассматривается как упругое вязкое тело,где результирующее
напряжение а является вязким телом.: С=ее+х е -^ -. (16.12) 516 где x упругого вязкого тела представляет некоторую константу, называемую коэффициентом вязкого трения. Эта гипотеза приводит к тому, что действие внутренней силы сопротивления при колебании пучка, рассматриваемого как система с определенной степенью свободы, заменяется действием внешних сил? =- K (коэффициент пропорциональности между силой и скоростью), приложенный в точке фиксации массы. Гипотеза Фойта удобна с точки зрения математического решения задачи, но, как показывает эксперимент, этот вопрос, объясняющий неупругое сопротивление материала п
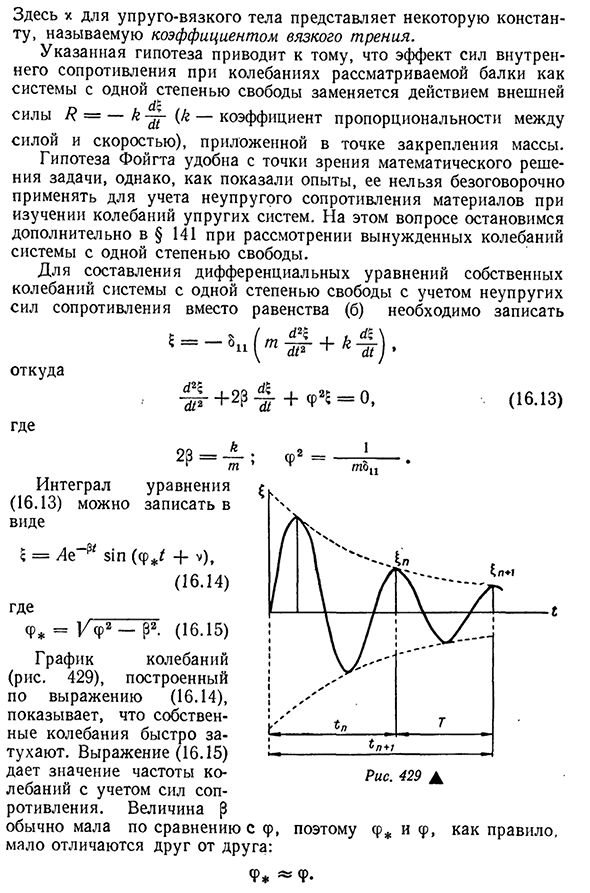
ри исследовании колебаний упругой системы, будет рассмотрен далее в§141 при рассмотрении вынужденных колебаний систем с определенной степенью свободы. Для составления дифференциального уравнения собственных колебаний системы с определенной степенью свободы с учетом неупругого сопротивления вместо равенства (b) можно записать: 6= — 8П(Т^+* -^). Откуда + 2 3+Г(Л=О,(16.13) Куда? 23= — ; Интеграл уравнения (16.13) можно записать в виде e=AC®81P(f*+V), (16.14) Где f= / F2-Z2 — (16.15)график колебаний (рис. 429) строится по формуле (16.14) и показывает, чт
о собственные колебания быстро исчезают. Формула (16.15) дает значение частоты колебаний с учетом силы сопротивления. Размер P обычно отличается друг от друга, маленький и маленький: Рис 429А По сравнению с P, CPи f являются, Ф Для оценки скорости затухания 517 мы находим отношение двух массовых отклонений, измеренных после одного цикла T(рис. Четыреста двадцать девять): Б_ _ _ _
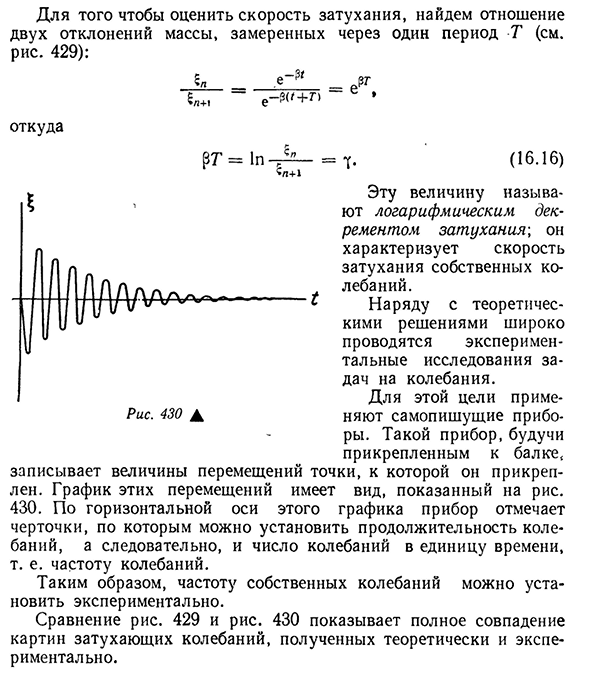
е~3<_6<_e-р (‘+г>е * Откуда 7. (16.16)) Один. г Рис 430А Это значение называется логарифмическим затуханием затухания и характеризует скорость затухания собственных колебаний. При теоретическом решении широко проводится экспериментальное исследование вибрационной задачи. Для этого используется самопишущее устройство. Такой прибор крепится к балке и фиксирует величину перемещения точки, на которой он установлен. График этих движений имеет вид, показанный на диаграмме. 430 горизонтальн
ая ось этого графика показывает линию, которая позволяет задать длительность вибрации, а следовательно и частоту вибрации в единицу времени, то есть частоту вибрации. Поэтому частоту собственных колебаний можно установить экспериментально. Диаграмма сравнения. 429 и рис. На рис. 430 показано идеальное совпадение моделей затухающих колебаний, полученных теоретически и экспериментально.
Смотрите также:
| Удар движущегося вагона о тупиковое ограждение | Вынужденные колебания упругой системы |
| Понятие о волновой теории удара | Общие понятия о концентрации напряжений |

