Рассмотрим геометрический смысл частных производных

Частные производные

• Частные деривативы Глава V111 показала, как искать функцию, используя производные. Для изучения функции многих переменных было введено понятие частных производных. Частная производная функции W = F (x> y, z) по переменной определения x является производной, рассчитанной в предположении, что все независимые переменные, кроме x, имеют постоянное значение. TT * dW dF Частная производная по x обозначена ^.

Или F (xy y y z). dF dW g * Другие независимые переменные воды: ^, -, гу dF dW Указывает частную производную по y. ,> R z — частная производная по z. Пример 1. Вычислить частные производные для всех независимых переменных функции z = xz + xy *. Предположим, что x переменная, а y постоянная. Затем, используя правила вычисления производных (см. Главу VII, §4), вы получите: | = 2 * + /. Как хорошо дз р

Конкретные производные определяются аналогично. Людмила Фирмаль

Пример 2. Найти частную производную функции W = xs \ n (y2 + z). Dw. / т, вд \ в 0 / 2,4 ^ / г, х ^ = sin (/ + z), ^ = 2 # ycos (y + z), = * cos (jr + z). Определение Частичное приращение функции z = r.F (x, y) по отношению к x — это приращение функции, вычисленное в предположении. Например, если указана функция r = ;; 2 + ^ ^ y, то это конкретное приращение «; найти это: дать l. Увеличьте h = & x и оставьте все как есть

Вычитая начальное значение другой переменной y, z + Az = (x: + Ax) r + y \ function дает: Az = [(x + Ax) 1 + y] — [xr + y] = 2x Ax + Ax1. Это конкретный прирост х. Другие частичные приращения определяются аналогично. Из определения частных производных (см. Определения производных в главе VII, § 3), частные производные по x имеют тенденцию иметь частичные приращения и приращения по x, при условии, что приращение Ax стремится к нулю. Вы можете видеть, что это предел отношения Aj. (*) F (x + dl, y) -F (x, y) Ax

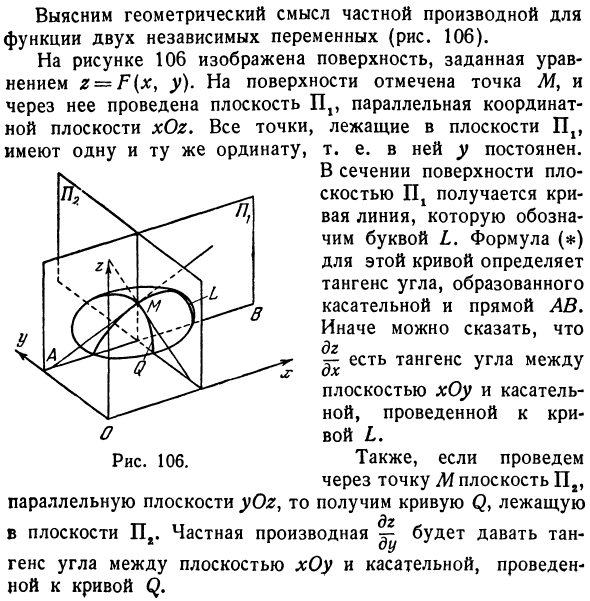
• Давайте рассмотрим геометрический смысл частных производных для функции двух независимых переменных (рис. 106). На рисунке 106 показана поверхность, определяемая уравнением z = F (Xy y). Точка M> отмечена на поверхности, а плоскость Pr проведена параллельно координатной плоскости xOz. Все точки в плоскости Px, Другими словами, вы постоянны. В сечении поверхности плоскостью P1 получается кривая, обозначенная буквой L.

Эта формула кривой (*) определяет тангенс угла, образованного касательной и линией AB. В противном случае, вы можете сказать, дз ^ Касательная угла между Касательная, нарисованная на плоскости xOy и кривой L Если вы проведете плоскость П2 параллельно плоскости yOz через точку M, вы получите кривую Q. В самолете Р8. Иметь одинаковую ординату Рисунок 106.

Частная производная ^ дает тангенс угла между плоскостью xOy и касательной, нарисованной на кривой Q. Людмила Фирмаль

Указывает на использование частичной дифференциации. Для этого сначала приведем несколько определений. значение функции z = F (x, y) для xa и y = i, то есть z = F (ay b), больше, чем все значения функций x и y, которые почти совпадают с a и b соответственно Называется максимум. То есть вы можете найти часть плоскости xOy, которая содержит точку (a, b) внутри, и функция меньше, чем F (a, b), за исключением (a, b) в любой из внутренних точек у вас есть. Минимальное значение функции определяется аналогичным образом.

Значение функции называется минимумом x = a, y = bf, если оно меньше всех значений x и y и почти совпадает с a и b соответственно. Например, минимальное значение функции z = x * — {- yy равно 0. Если x = 0 и y = 0, функция равна 0, а другие значения x и y положительны, т.е. больше нуля (см. Главы VIII и 3). Геометрически очевидно, что максимальное значение функции определяет точку над смежной точкой, а минимальное значение определяет точку ниже смежной точки. При использовании географических терминов максимальное значение функции определяет вершину горы, а минимальное значение — низменность.

Также геометрически ясно, что тангенс вершины, нарисованной на кривой, проходящей через вершину, параллелен плоскости xOy. О дз дз Следовательно, верхние (и нижние) частные производные ^ и ^ равны нулю (см. Главу VIII, §3). Однако в какой-то момент частная производная может быть равна нулю, но нет максимального или минимального значения. Такая точка называется седлом. Например, поверхность показана на рисунке. 107, происхождение Седло есть. Фактически, сечение с плоскостью xOz даст кривую с минимумом в начале координат, а сечение с плоскостью yOz даст кривую с максимумом в начале координат.

Частная производная дг дг ^ И ^ равны нулю, но на поверхности нет максимального или минимального значения. Если существование максимальных или минимальных значений определено, их можно найти с помощью частных производных. Пример 3. Найти параболическую точку z = x * — {- yy, точку M ^ 16, ближайшую к 0, Сначала посмотрим, находится ли точка М на параболоиде. Если это так, он попросит об этом. В противном случае расстояние от точки М до любой точки на параболоиде всегда будет больше нуля. Подставляя координаты x = 16, y = 0, z = в параболическое уравнение, получаем Ф162 + О2. Следовательно, точка М На параболе. Далее рассмотрим любую точку на параболоиде. x и y произвольны, а z можно найти из уравнения z = x2 + y2. В результате координаты любой точки P на параболоиде имеют вид (i, y, x2 + >> ). Создайте выражение, представляющее расстояние между точками M и P (см. Выражение () в главе 2 этой главы). M P =) / (* -16) 2 + 0′-0) 2+ (* «+ / — ^ Y-

Это расстояние (эта функция) никогда не равно нулю, как мы видели ранее, но может быть сколь угодно большим. Если частная производная исчезает в любой точке, минимальное значение возможно в этой точке. Если расстояние минимально, квадрат также является минимальным значением. Поэтому вместо расстояния MP рассмотрим этот квадрат. На это указывает буква W. Поэтому возникают следующие проблемы: Найти минимум функции W = (x-16) 2 + (L; 2 + /

Рассчитаем частную производную: Сделайте их равными нулю: 2 (x — 16) + 2 (* »+ / — = Решить полученные уравнения одновременности —16 + 2l, 8 + 2xu2 = 0, Y (** + /) = <>. Из второго выражения, если y = 0 или π1 + .y2 = 0 >> >> 0, получить 2n из первого выражения, 8 —16 = 0 и x = 2. Однако 0, тогда x = 0 и) «= 0; если присвоено первому выражению, -16 = 0, то есть эти значения ему не удовлетворяют, поэтому системное решение равно x = -2, только y = 0. В результате параболическая точка, ближайшая к точке M ^ 16, 0, найдено, это P (2, 0, 4).

Смотрите также:

Предмет высшая математика

Поверхности	Семейство функций
Линии уровня	Основные определения