Оглавление:



Понятие о волновой теории удара
- Концепция теории ударных волн 0 Метод расчета воздействия, основанный на замене бесконечно большой системы системой степеней свободы, описанной в предыдущем пункте, является приближенным. Степень приближения ко многим. Многие случаи
неизвестны. Чем больше жесткость системы, подлежащей удару, тем менее достоверен результат, полученный из расчетной формулы. Так, например, при продольном ударе мобилем по стержню
призмы результаты теории расходятся больше с экспериментальными Людмила Фирмаль
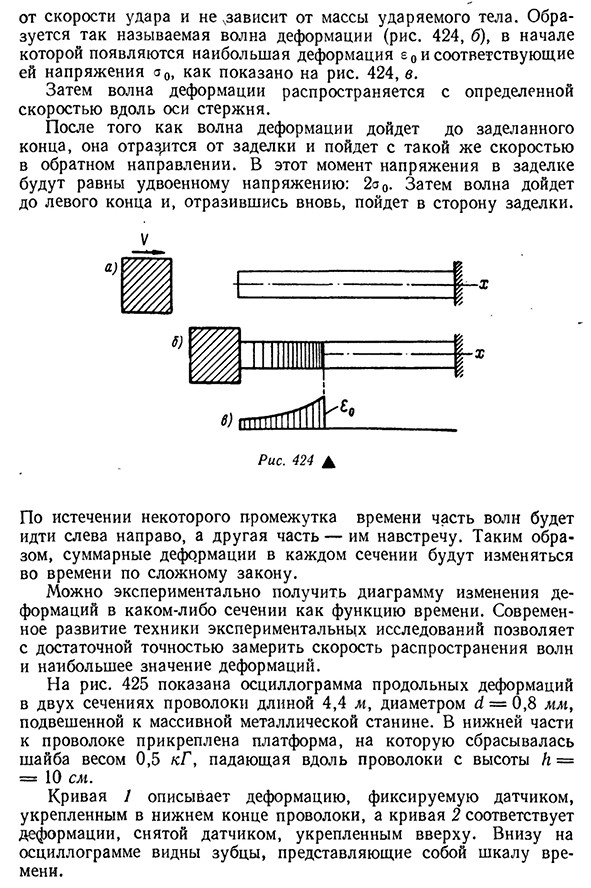
данными, чем с поперечными. Более точный результат можно получить, рассмотрев теорию ударных волн. Рассмотрим эффект, если абсолютный твердый объект, движущийся со скоростью V по стержню, строго запечатан с одного конца(рис. 424, а) исследование
этого вопроса показывает, что сжимающая деформация, возникающая в первый момент удара, является 510½ лежачий полицейский, не^зависит от массы удраого тела. Образуются так называемые деформационные волны(рис. Рис. 424, б), наибольшая деформация e0 и соответствующее напряжение a0 появляются
- первыми. 424, ст. В свою очередь, деформационная волна распространяется с постоянной скоростью вдоль оси стержня. После того, как волна деформации достигает запечатанного конца, она отражается от уплотнения и идет с той же скоростью в противоположном направлении. В это время напряжение на уплотнителе равно удвоенному напряжению: 2A0. После этого волна достигает левого края, снова отражаясь и направляясь к уплотнению
. В Два. Икс Л Икс Я б)gtggtgtgtgt Рис 424Л Через некоторое время одни волны движутся слева направо, другие им навстречу. Таким образом, общая деформация каждого участка изменяется во времени по сложным законам. Экспериментально можно получить диаграммы деформационных изменений любого сечения в зависимости
от времени. Современное развитие методов экспериментальных исследований позволяет с достаточной точностью измерять Людмила Фирмаль
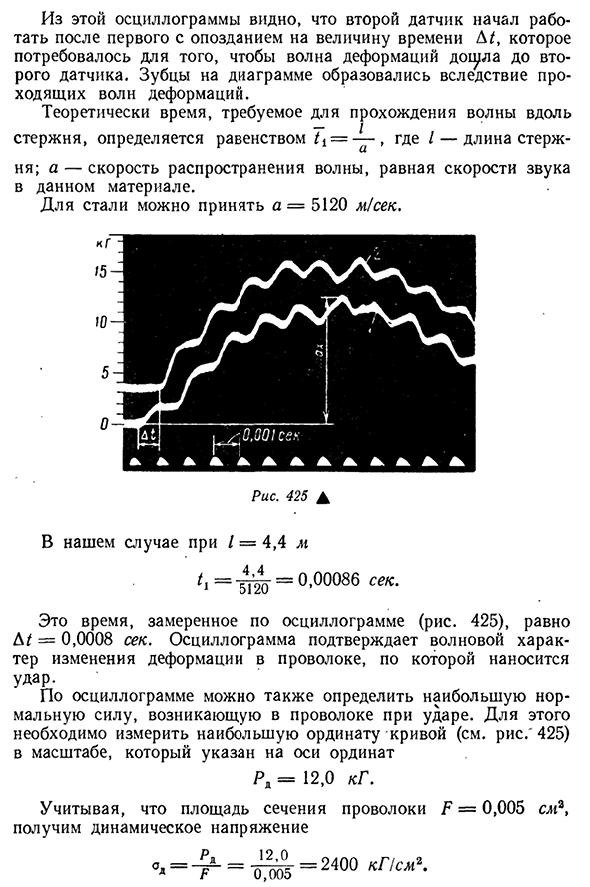
максимальную скорость распространения и деформацию волн. Для риса. На рис. 425 показана осциллограмма продольной деформации в двух сечениях проволоки длиной 4,4 м и диаметром<1=0,8 мм, подвешенной к огромному металлическому каркасу, дно проволоки, прикрепленной к платформе, сбрасывает 0,5 кг шайбы и падает вдоль проволоки с высоты H= — 10 см. Кривая 1 представляет собой деформацию, записанную датчиком, прикрепленным к нижнему концу провода, кривая 2 захватывается датчиком, прикрепленным к верхней части нижней части формы волны деформации имеет
видимый Зубец, представляющий временную шкалу. 511 из этой формы волны второй датчик начал работать после того, как первый с задержкой/время, которое требовалось для того, чтобы волна деформации достигла второго зубца датчика на диаграмме, было сформировано в результате прохождения волны деформации. Теоретически время, необходимое для прохождения волн вдоль стержня, определяется уравнением=—, где I-длина стержня. Для стали можно взять=5120 м/с. Рис 425А В нашем случае 1=4,4 м= — ^P20-0>00086 в секундах. Это время измеряется осциллограммой (рис. 425), равный
а / =0,0008 секунды.форма волны подтверждает волновую природу изменения деформации поражаемого провода. Осциллограмма может также определить максимальную нормальную силу, которая возникает на проводе при ударе. Для этого измерьте максимальную ординату кривой (см. рис.’425)в масштабе, указанном на вертикальной оси Rd=12,0 кг. Учитывая, что площадь поперечного сечения провода составляет Р=0,005 см2, динамическое напряжение а » = = — DY — =2400 кгс!см2. 512P12 Динамический коэффициент p= = 24. Для сравнения, попробуйте найти динамический коэффициент по
формуле (16.3). Удлинитель провода 0.5-440 2,1 106,0,005 =0,021 см. Масса платформы на конце провода 6 0=0,475 кг. Отсюда-0,95. Высота падения H=10 см. Назначение выражения (16.3) выглядит следующим образом Один. 1+0,95 =23.1. Результаты очень близки друг к другу. Интересно отметить, что по мере уменьшения значения O0 разница увеличивается. При малых значениях O0 найденные экспериментально динамические коэффициенты практически не зависят от массы падающей нагрузки, что хорошо согласуется с волновой теорией удара.
Смотрите также:
| Расчеты на удар | Собственные колебания системы с одной степенью свободы |
| Удар движущегося вагона о тупиковое ограждение | Вынужденные колебания упругой системы |

