Расчет составных стержней на продольный изгиб

Оглавление:

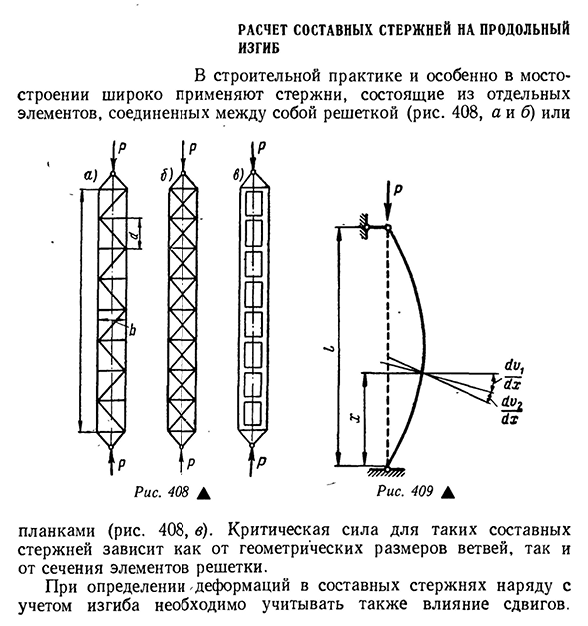
Расчет продольных композитных стержней Сгибать В строительной практике, особенно в мостостроении, широко используются бруски, состоящие из отдельных элементов, соединенных решетками(рис. 408, а и в) или Рис 408А Доска (рис. 408, в). Критические силы такого композитного стержня зависят как от геометрических размеров

ветвей, так и от поперечного сечения элемента сетки. При определении деформации композитного стержня необходимо учитывать изгиб, а также влияние сдвига. Если расстояние между узлами 489 решетки C1 мало по сравнению с длиной I, то можно применить приближенный расчет, состоящий в том,

что составные стержни заменяются обычными сплошными стержнями, поэтому Людмила Фирмаль

рассмотрим сначала задачу учета смещения сплошных стержней(рис. 409). Отклонение стержня в любой точке может быть выражено как сумма двух отклонений: ^=^+^2″(15.30) Здесь отклонение вызвано изгибом, а O2-отклонение, вызванное сдвигом. Точно так же (IV(1U1, (1U2 ЫХ-ЫХ Угол поворота сдвига пропорционален боковой силе и

обратно пропорционален модулю сдвига и площади поперечного сечения t’Wed » Здесь K-коэффициент, учитывающий неравномерное распределение напряжения сдвига по всему сечению, которое зависит от формы сечения. И так оно и есть., (1u2_ _ _ с(1м «ИГ~ ~ СР ~ ~ СР’ (15.31) И так оно и есть., A2U2_ _ to CPM AH2-CP * AH2 * Если вы

думаете, что уравнение определено здесь От дифференциации Sruh м~1x2E Т’ Тогда мы получаем (Ру (Рух. sru2M yh2yh2AH2E^, K (RM+SR’AH2 * В нашем случае CPM_ _ Р сру yx2<1х2′ 490 это уравнение: наконец, мы имеем следующие производные Или ^ +, Т2! о=п0. (15.32) Куда? Неотъемлемый Два. П Т Ы(В Р’ Уравнение (15.32) известно как& — A pop TX-B at 81p TX. (15.33) Граничное условие x=0, V=0; x=I, V = 0 Дай А=0; 51P T1=■в 0, значение не может быть нулевым (в этом случае нет

отклонения). z1p T1=0. Это состояние может существовать при Т1=к, 2К, ЗК, ИК. Определить наименьшую критическую силу、 ТС Т= -. Тогда вы получаете от равенства после простого преобразования(15.33 TS2 2? / ____1____ /и нанять 1 ‘+~0Е~1Г — = * Р,(15.34) Куда? И= Один. 14-Ал!^ После прибытие 491 таким образом, мы можем видеть, что критическая сила, учитывающая сдвиг, меньше силы Эйлера, поскольку A<1. Ае~6р~’~Р(Г’~Р~0~’) Р9 Тогда a определяется выражением Тогда возьмем 6=800 000KP CM / OCR / tah =

opt=2000kpsm2 Учитывая, что значение K в большинстве сечений близко к единице, Людмила Фирмаль

мы обнаружили, что для непрерывных сечений сдвиг мало влияет на критические силы. Если перейти к рассмотрению композитного стержня, то картина резко изменится. Определить величину угла сдвига в одной панели составного стержня, имеющего стержень, от поперечной силы F. Для риса. 410, отображать одну панель с боковым усилием (}. Мы предполагаем, что доски имеют гораздо большую жесткость, чем ветви, поэтому их деформацией пренебрегают. В этом случае в центре высоты ветви имеют точку перегиба и, соответственно, отклонение от точки с(Рис. 410, б) можно определить как в консольной балке: I_M3 8\2\2/_(RC 2.) ZEEW48E/Ш’ Где 7B-момент инерции ветви относительно ее оси. Итак, если эту величину

сравнить с углом сдвига твердого стержня, который определяется по формуле (15.31), то роль величины здесь играет величина■24^7•*. Один. Один. А2 24E. GW24 / 2 / V Где / St-момент инерции всего поперечного сечения стержня. Если момент инерции выражается через радиус инерции, то для стержня, состоящего из двух ветвей, И для ответвления к собственной центральной оси Затем подставьте значение момента инерции в полученное выражение для RCR: Ре

Учитывая, что в баре есть гибкость Окончательно получить РЕ 1+0.83 ул HST здесь-гибкость всех ядер; H В — Гибкость ветвей в одной панели. Для упрощения формулы вместо резерва 0,83 принимаем 1: О~Р * _CR-As2t+Х2 ‘ * ст 493gde Когда теперь указывать Тогда мы получаем П * КСТ = ^ПРИВ» Такая формула для определения снижения гибкости композитного стержня приведена в СНиПе для конструкции моста. Если не учитывать эффект смещения составного стержня, то серьезные силы сильно переоцениваются. Это может привести к неточному учету грузоподъемности сжатого стержня, и в связи с этим произошло разрушение Квебекского моста на реке Святого Лаврентия.

Смотрите также:

Учебник по сопротивлению материалов: сопромату

Практический расчет сжатых стержней	Динамическое действие нагрузок общие замечания
Продольно-поперечный изгиб	Учет сил инерции при расчете троса