Оглавление:




Графо-аналитический способ определения радиальных перемещений в кривом брусе
- График-как анализировать решение Радиальное перемещение криволинейных балок Графоаналитический метод определения смещения в прямой балке (см.§82)был основан на подобии
Дифференциальные уравнения, связывающие изгибающий момент с нагрузкой, *M_AH2 В случае криволинейных стержней, которые очерчены в виде круга, можно видеть, что есть также
Сходство между двумя аналогичными уравнениями. В предыдущем пункте было Людмила Фирмаль
получено дифференциальное уравнение радиального перемещения (14.19). Как только вы дифференцируете это уравнение、 * + — «4 тонны. а) asr3ASR ASR I EA]’ Аналогичное дифференциальное уравнение (14.5) было получено в§119: (бел) Сходство уравнений
(а)и(Б) — это одна задача, которая определяет радиальное отклонение, которое должно быть уменьшено для построения точки от фиктивной нагрузки и заменено другим., м е^ • Эта фиктивная нагрузка должна быть приложена к радиальной фиктивной балке. Для достижения
- точного равенства Ю=м ф , Такие граничные условия, соответствующие граничным условиям отклонения, должны быть созданы на воображаемом стержне. Обратите внимание, что для криволинейных стержней справедливо равенство 453можно утверждать, что угол поворота поперечного сечения криволинейной балки определяется как мнимая поперечная сила: Ф= s1sh(1М&<ЛЗ<ЛЗ За столом. На рисунке 17 показан пример фиктивного стержня,
который соответствует стержню с определенным фиксированным концом. Так, например, брусок, запечатанный на одном конце, подобно прямому стержню, в фиктивной системе пломба переносится на другой конец. Если балка является закрученной опорой, то фиктивная система совпадает с данной системой, в то время как стержень подвижной опоры расположен радиально. В других случаях проблема выбора фиктивной системы должна решаться каждый раз
отдельно. Правила знака в методе анализа графов для криволинейного пучка остаются теми же,что и для прямого пучка, а именно:графики M и Людмила Фирмаль
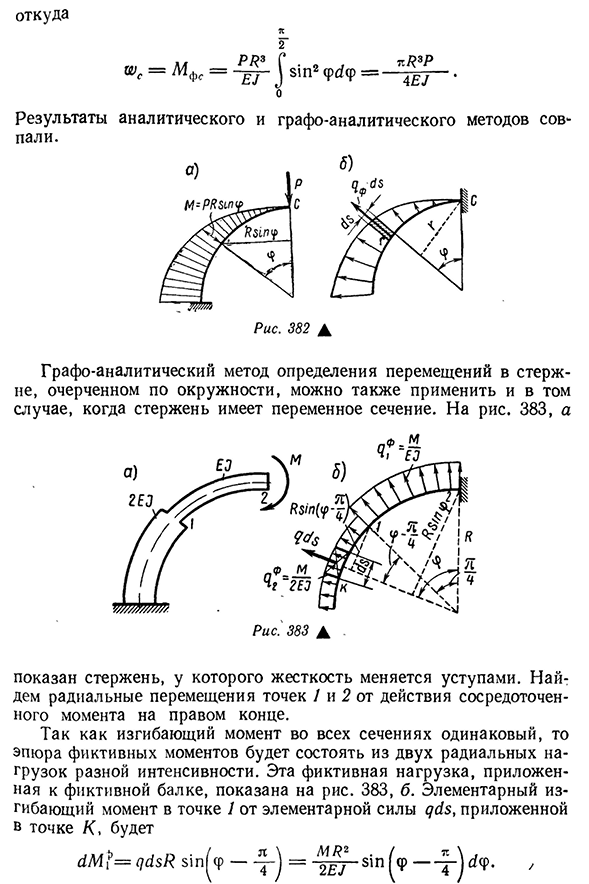
L4f строятся со стороны растянутого волокна. Рассмотрим тот же пример, который был аналитически решен в предыдущем абзаце. Для риса. 382, показывает график момента в данной системе. Для риса. 382, b показывает кривую воображаемого луча. Нахождение вымышленного момента в C 454 откуда угодно Л И,=2 2ghf. * 9х3р ] 81p2f*R= — 4EG- • Отчет Результаты анализа так и упали. Как
поперечное сечение, то также может быть применен графоаналитический метод определения смещения в стержне, который очерчен кругом. Для риса. 383, а Показан стержень, жесткость которого изменяется в зависимости от выступа. Найти радиальное смещение точек 1 и 2 от действия самого правого сосредоточенного момента. Поскольку изгибающий момент всех сечений одинаков, график мнимого момента состоит из двух радиальных нагрузок разной интенсивности. Фиктивная нагрузка на фиктивную балку показана на рисунке. 383, b. базовый изгибающий момент точки 1 базовой силы^$, приложенной к точке K, равен p4º
дает возможность определить величину мнимого момента в точке/. она равна величине радиального отклонения в данной точке: Два. л ТС Четыре. тс тс Четыре. _ _ _ _ _ _ _ _ -2. 0, 15M7?Два. Ми^ Для точки 2 плечо базовой силы равно 7? 81p Ф,воображаемый момент,и, таким образом, вертикальное отклонение встречается в виде суммы двух интегралов: И и т т т .Ф М р г. . Ы, ы, ы, ы, ы, ы, ы 81P FB/f4-81P fygf= А про т_м/?2р, МФ п оо<3_0. 646L4/?Два. 2Е^Я,/Я/Е/~ЭЛ Аналогичным образом можно определить радиальное отклонение стержня, жесткость которого непрерывно изменяется по его длине. Фиктивная
нагрузка любой секции равна моменту, принятому в этой секции M9, деленному на жесткость этой секции EU^: Если стержень очерчен на какой-либо кривой, например, в некоторой степени близкой к окружности на параболе, то для аппроксимации решения задачи применяется та же техника. Воображаемый момент воображаемого Луча даст кривой смещение точки вдоль нормали.
Смотрите также:

