Оглавление:



Чистый изгиб кривого бруса
- Чистый изгиб Кривого бруса Для определения давления чистого изгиба плоского стержня кривой, а также для прямого стержня, мы можем обеспечить плоский стержень кривой кривой с G и n O t E z u n l o S K и x s e h Определяя деформацию волокон балки, мы игнорируем радиальные напряжения. Рассмотрим стержень-на поверхности
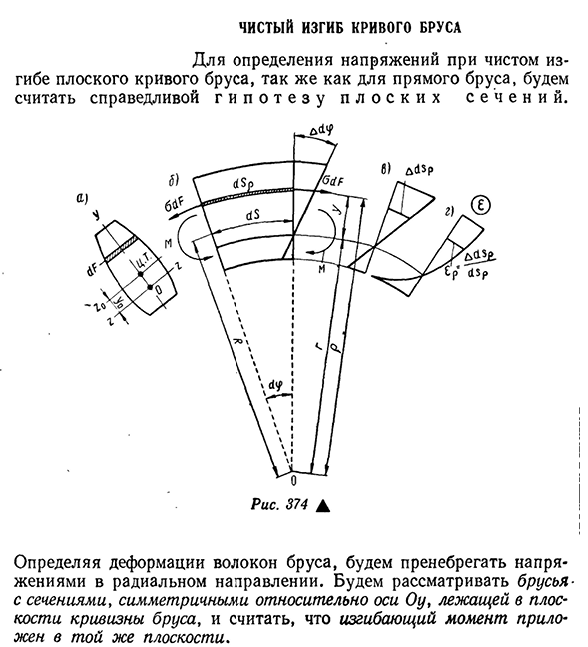
кривизны стержня, вокруг оси Oh в сечении симметрии, и предположим, что изгибающий момент приложен к той же плоскости. 440, рис. 374 показана длина балочного элемента (15 имеет симметричное поперечное сечение(фиг. 374, а, б).
Ось выхлопного газа направлена вдоль нейтральной оси, где секция вращается. Людмила Фирмаль
График показывает абсолютное удлинение волокон на рисунке. Рис. 374, Б, и фигуры удлинения показаны на рисунке. 374, г. Абсолютное удлинение высоты сечения изменяется по закону прямых линий, а также по закону кривых (гипербола). Это связано с тем, что значение длины дуги=rysr также изменяется по высоте, поэтому для любого волокна вдали от нейтрального слоя на расстоянии y、 _что такое
решение? ‘g er_R+г’ Предположим, что волокна находятся друг на друге. Согласно закону крюка, не нажимайте г г+г’ (14.6) Потому что в чистом изгибе нет нормальной силы Или рассмотрим(14.6)、 Но так как множители перед интегралом не могут быть равны нулю、 (14.7) п Равенство (14.7) является условием для определения местоположения
- нейтрального слоя. Тогда получается, что в последнем случае статический момент / UIR, E должен быть равен нулю, чтобы нейтральная ось криволинейного луча не проходила центроид Потому что это было для прямой штанги (см.§66). Теперь выразим момент внутренней силы относительно нейтрального слоя через напряжение и приравним его к внешнему моменту, принятому по абсолютной величине: (14.8) Э Э Э 441 ° (14.8), содержащееся в
выражении, может быть представлено в следующем виде Так как второй член полученного уравнения с уравнением (14.7) равен нулю、 (14.9) Где 8 g=Ru o-статический момент площади поперечного сечения относительно нейтральной оси (y0-расстояние от центроида сечения до нейтральной оси). Если вы назначаете (14.9) эквиваленту (14.8)、 М=е~8г. И так оно и есть., ды<Р М А? ~E8g’ * (14.10))
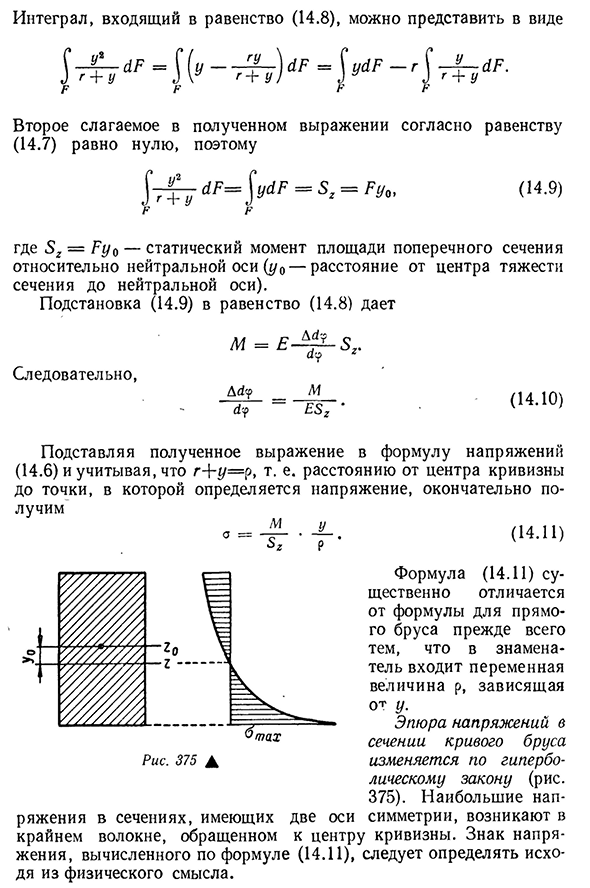
Подставляя полученную формулу в Формулу напряжений (14.6), мы учитываем расстояние от g+g/=p, то есть от центра кривизны до точки, в которой определяется напряжение, получаем в итоге (14.Ньютон) Формула Людмила Фирмаль
(14.11) существенно отличается от формулы для прямых столбиков тем, что знаменатель содержит переменную p, зависящую от Y. Диаграмма напряжений в поперечном сечении криволинейной балки изменяется по гиперболическому закону(рис. 375). Максимальное напряжение в поперечном сечении с двумя осями симметрии возникает в крайних волокнах, обращенных к центру кривизны. Знак напряжения, рассчитанный по формуле (14.11), должен определяться исходя из физического смысла. Чтобы сравнить прямые и кривые формулы для 442÷brush s, преобразуйте формулу(14.11). Из(14.9) находим U2 Покажите Этот Интеграл
называется моментом инерции поперечного сечения криволинейной балки. Верхний значок в виде дуги служит характерным знаком от обычного осевого момента инерции. При/■ — >OO легко заметить, что момент инерции изогнутой балки в пределах предела совпадает с нормальным осевым моментом инерции. И так оно и есть., 52=4-l — <14-12) Если вы присвоите это выражение выражению (14.11), и P=g+y、 Около (14.13) L14s. 7г В случае G->OO выражение в пределе (14.13) совпадает с нормальным выражением прямого луча. В§123 приведена сравнительная таблица результатов, полученных по двум формулам: для кривых и прямых стержней.
Смотрите также:

