Вычисление давления жидкости

Вычисление давления жидкости

• Расчет давления жидкости Давление жидкости на погруженную в нее горизонтальную тарелку равно весу этого столба жидкости с дном тарелки, а высота — это расстояние тарелки от свободной поверхности жидкости. Давление обозначается буквой Р, удельный вес у жидкости равен площади плиты, расстояние А от свободной поверхности жидкости до плиты; P = y SH. На языке этого закона важно, чтобы табличка была горизонтальной.

Расстояние между параллельными плоскостями точно определено. Если пластина не горизонтальная, вам нужно поговорить о расстоянии между двумя непараллельными плоскостями. Но что это значит? Вот как можно решить проблему, когда пластины расположены вертикально. Задача 1. Опустить пластинку в форме круга с радиусом R в жидкость с удельным весом, равным y.

Поверхность жидкости также считается горизонтальной плоскостью. Людмила Фирмаль

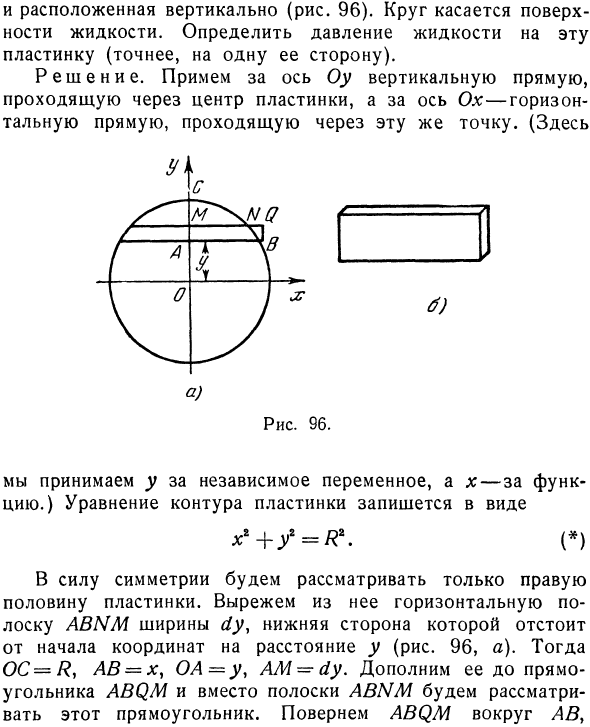
Разместите их вертикально (Рисунок 96). Круг касается поверхности жидкости. Определите давление жидкости на этой пластине (точнее, на одной стороне). Решения. Рассмотрим вертикальную линию, проходящую через центр пластины на оси Oy, и горизонтальную линию, проходящую через ту же точку на оси Ox. (Нажмите здесь Ничего себе! а) и H /// 7 М ^ 4 (А к-чу \ 0 1 * г) Рисунок 96.

Используйте y для независимой переменной и x для функции. ) Уравнение контура пластины записывается в следующем формате: х * + / = /? «(*) Из-за симметрии рассматривается только правая половина пластины. Горизонтальная полоса ABNM шириной dy вырезана из нее, а нижняя сторона находится на расстоянии y от начала координат (рис. 96, а). Далее OS = ?, AB = x, OA — y, J — dy. Добавьте это к прямоугольнику ABQM и рассмотрите этот прямоугольник вместо полосы ABNM. Включите ABQM в AB>

• Дайте ему горизонтальное положение. Теперь вы можете применять законы, перечисленные в начале этого раздела. Возьмите ряд жидкостей с основным прямоугольником ABQM (горизонтальное положение). Высота — это расстояние AC до поверхности жидкости. Объем столбца AC * AM * AB = (R — y) xdy, а вес — yx (R — y) dy. Это количество называется основным давлением и выражается в дП. так dP = \ x (R-y) dy.

Пределы интегрирования указывают минимальное и максимальное значения y на табличке. Ниже знака интегрирования находятся две переменные, x и y. Исключите x из выражения (*), указав его как y. тогда R __ P = Jy (R-y) VR2-fdy. -R Преобразовать интеграл: R P = Y J (R-y) VW ^ 7dy = -R R R = y 5 R y R2 — y2 dy-y S yVR2 — yzdy = -R -R R R = yR $ VR2 — y * dy — y 5 yVR2- / dy. -R -R

Интегрируйте в диапазоне от -R, чтобы получить желаемое давление. R P = J Yx (R — y) dy. -R Людмила Фирмаль

Применение результатов, полученных в §§ 2 и 3 гл. 3 X, есть:R -R -R D2 ftZ = arcsin 1 —arcsin (- {) = -n, R R = 0 -R yVRf— / dy = -R R2 я /? 3 Поэтому, наконец, P = yR — n — Y ‘^^ Y- ^ «* Таким образом, половина давления жидкости в пластине (справа) vjt R * Равное давление на пластине

Смотрите также:

Предмет высшая математика

Объем тела вращения	Вычисление работы силы
Объем тела, у которого известны площади поперечных сечений	Длина дуги