Оглавление:




Объем тела, у которого известны площади поперечных сечений
- Объем тела с известной площадью поперечного сечения Рассмотрим тело, расположенное так, как показано. 94. Объем этого тела обозначен V. Давайте назовем сечение этого объекта формой, которую вы получите, когда он пересекает вертикальную плоскость Площадь каждого поперечного сечения 5 (х) известна. В этих условиях определяется объем тела. Для этого возьмем два поперечных сечения друг от друга на расстоянии h = dx. Рассмотрим два цилиндра.
Оба цилиндра имеют одинаковую высоту (дх). Объем объекта между указанными сечениями является приращением объема V. Представлено ДК. Этот прирост больше, чем объем первого цилиндра, и меньше, чем объем второго цилиндра.
Первый цилиндр имеет левую часть в качестве основания, а второй — с правой стороны. Людмила Фирмаль
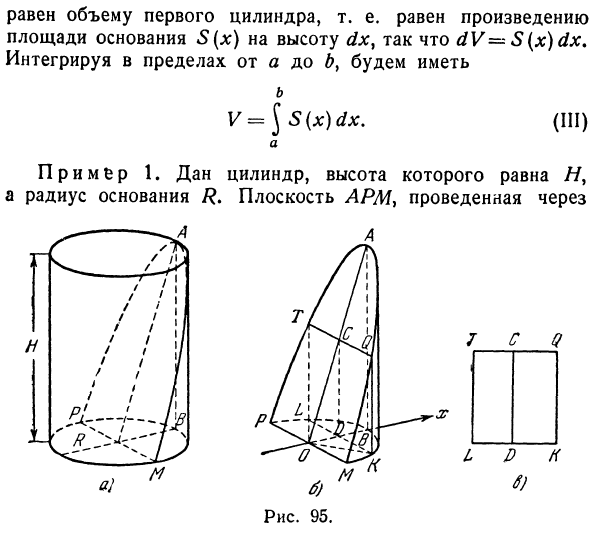
Аналогично §1, 3 в этой главе, производная d V Поскольку он равен объему первого цилиндра, то есть произведению базовой области 5 (x) и высоты dxy, он равен dV-S (x) dx. Интегрировать в диапазоне от а до б} б V = \ s (x) dx. (Болезнь) но Пример 1. Дан цилиндр с высотой // и базовым радиусом R. Рисунок 95
Диаметр основания пересекает этот цилиндр (Рисунок 95). Определяет объем мелкой детали, вырезанной в плоскости, то есть объем детали MPA. Нарисуйте отдельные нарезанные кусочки (Рисунок 95, б). На этом рисунке OP = OM-OB-? , AB = AND, KL = KD + DL = 2KD. Занимает прямую линию, перпендикулярную диаметру и в плоскости днища цилиндра относительно оси Ox.
- Тогда OD = х. Нарисуйте сечение KLTQ. Он прямоугольный (рис. 95, в). Площадь KL »DC. Выражается с помощью х. Найдите КД из прямоугольного ОДК треугольника. KD = Y0Kx-OD * = VR1 — xr, следовательно, KL = 2
От-следовательно площадь поперечного сечения г-_ S = —x) //? 2 — Применение формулы (III), R V = J 2-x: V R1 — ** дх. () 0 Заменить для вычисления этого интеграла Это дает -2xdx = 2zdz и xdx — z dz. Если x = 0, новая переменная z равна, или если x = R, она равна 0. Если вы измените переменную на (), т. 2H, h 2H C, 2H (gp o 2 HR * R R
Из аналогичных треугольников ODC и OVA видно, что: CD _АВ9R-JL OD около 9 или х R * Людмила Фирмаль
Смотрите также:
| Площадь криволинейной трапеции | Вычисление давления жидкости |
| Объем тела вращения | Вычисление работы силы |

