Оглавление:


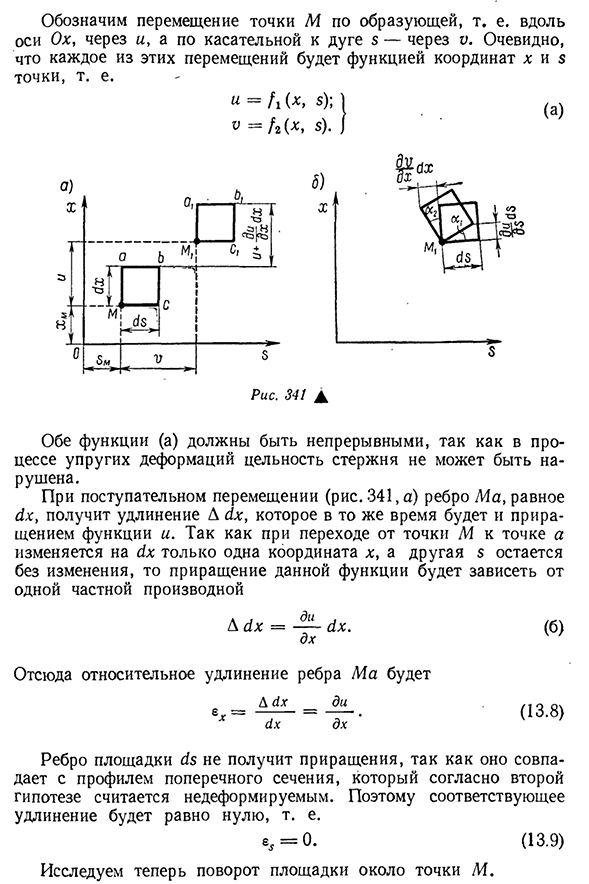



Зависимости между деформациями стержня и перемещениями его точек
- Износостойкость между деформациями Движение палки и ее точек При построении теории расчета тонкостенных стержней на кручение принимаются две основные гипотезы. Во-первых, предполагается, что деформация сдвига промежуточной поверхности стержня равна нулю. Другими словами, предполагается, что угол между двумя
прямыми линиями совпадает с центральной плоскостью, одна из которых образует, 397а и другие перпендикулярны ему, и при скручивании стержень не меняет своего значения. Согласно второй гипотезе, профиль поперечного сечения считается жестким
или недеформируемым. Под этим понимается проекция поперечного Людмила Фирмаль
сечения на плоскость, перпендикулярную оси стержня, при условии, что он сохраняет определенные размеры и форму в процессе деформации. Согласно этой гипотезе, деформацию стержня можно представить в виде серии витков поперечного сечения под углом вокруг определенного полюса,при которых каждое поперечное сечение одновременно испытывает истощение. Для исследования упругой деформации рассмотрим стержень с произвольной формой поперечного сечения, который находится в состоянии сдержанного
скручивания. Потому что напряжение имеет одинаковую толщину поперечного сечения (см. Рисунок). 337, Б), достаточно определить их для точки срединной плоскости. Для этого необходимо изучить движение точек, расположенных на промежуточной грани стержня, которая показана на рисунке. 340. Оси OU и Og берутся в сочетании с главной центральной осью инерции секции и осью Oh стержня. Возьмите любую точку M на промежуточной плоскости и выберите
- базовую область рядом с ней. Положение точки M определяется координатой XM и дугой 5m>, которая отсчитывается от некоторой начальной точки M0 на поперечном сечении*средней линии, проходящей через исследуемую точку m. Общее движение базовой площадки можно представить как состоящее из поступательных и вращательных движений вокруг точки М. История * Расположение точки m o зависит от формы профиля поперечного сечения и определяется на основе конкретных требований, описанных ниже
398 ясно, что каждое из этих движений является функцией координат x и 5 точек. Обе функции(а) должны быть непрерывными, так как в процессе упругой деформации целостность стержня не может быть нарушена. В этом случае 341, а)ребро MA, равное C1X, получит расширенный D C1X, который будет приращением функции I одновременно.С момента перехода из точки М в точку а остается только одна координата x Д ы/х=y х. Dн. Следовательно, относительное удлинение ребра Ма Восемь. Х’ ДХ ДХ ДХ (бел) (13.8)
Ди ДХ Кромки участка с/5 не претерпевают приращений, так как, согласно второй гипотезе, они совпадают с профилем поперечного Людмила Фирмаль
сечения, который считается недеформируемым. Таким образом, соответствующее удлинение будет равно нулю, то есть 8^=0. (13.9) Когда М рядом с платформой, 7 399 происходит последовательно в первой гипотезе об отсутствии сдвига в средней плоскости вращения платформы и без искажения прямого угла между ее краями(рис. 341, б). Отсюда и равенство углов: 1-А2-(13.10) Приращение для функций и и o выглядит следующим образом *: Ди= ДЗ Дю= — — — — — ДХ. DH. (В) Из рисунка. 341, б. Ди. < 4= ДЗ DH. Или согласно(13.10) Ди Ди ДЗ ДХ (13.11) Равенство (13>11) имеет две неизвестные функции I и o, которые необходимо определить. При скручивании стержня пусть поперечное сечение повернуто вокруг нескольких полюсов а(рис. 342, а) угол 6. Из положительного начала координат оси X примем положительный угол кручения 6, где сечение вращается против часовой стрелки. В
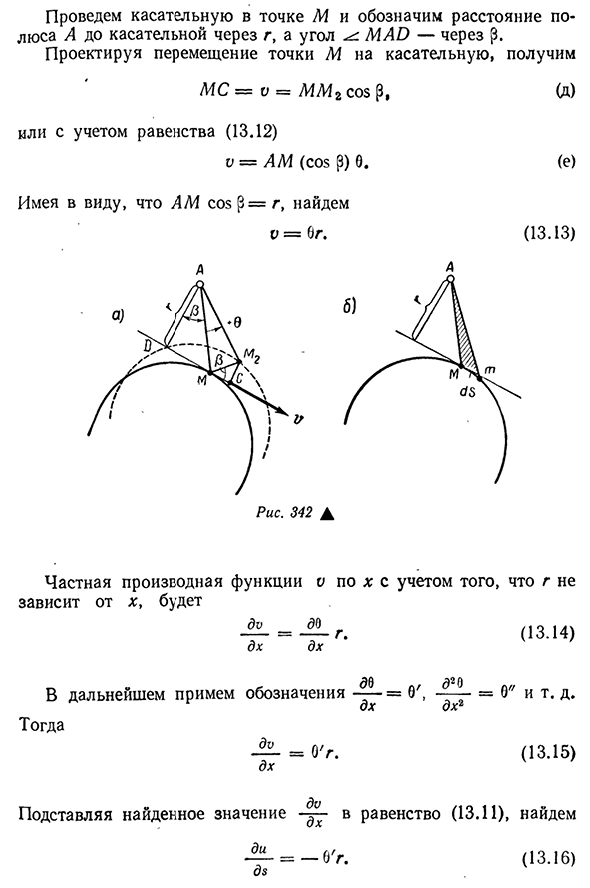
соответствии с гипотезой о недеформируемости формы сечения, последняя вращается как жесткий диск, а точка M перемещается в положение M2. Предположим, по малости угла 6, мм2=AMD. (13.12) История *Считается, что функция и приращение в точке перехода M на дуге 5 при постоянной координате x, и 5 пересекают одну и ту же точку на шине шины при постоянной координате с функцией. Знак минус в приращении функции ставится так, чтобы возникать в направлении отрицательной дуги 5. Проведем касательную с M и обозначим расстояние полюса A до касательной через g и угол Мао-через R. Когда смещение точки M проецируется на касательную, MS=V = M M g p, (d) Или равенство счетов(13.12) В=АМ (поп-Р) 6. (ми) Имея в
виду Am pop φ=g, мы находим В=6г(13.13) Если G не зависит от x, то частный дифференциал функции V над x равен Да для ДХ (13.14) В будущем мы будем принимать Затем Обозно — — — — — =о, ДХ Д2 и Д Н2 =6″и др. =О’г. DH. (13.15)) Присвоить найденное значение Д.§ Да, ДХ. Равенство (13.11)、 (13.16) Для получения функции 401 и выполнения Интеграла уравнения (13.16)дуга на дуге 5,заданной 6′,от дуги 5 не зависит. В результате получается and= = -0’y g+I0 (x). (13.17) в результате(13.17)была введена функция, независимая от I0(x) 5, поскольку здесь интегрируется частичная производная от h. В физическом смысле функция I0 (x) представляет собой часть смещения, которое одинаково для всех точек поперечного сечения. Произведение Gy&in-Формулы(13.17) представляет собой двойную площадь основного сектора АМТ, показанную на рисунке. 342, б.. Ес
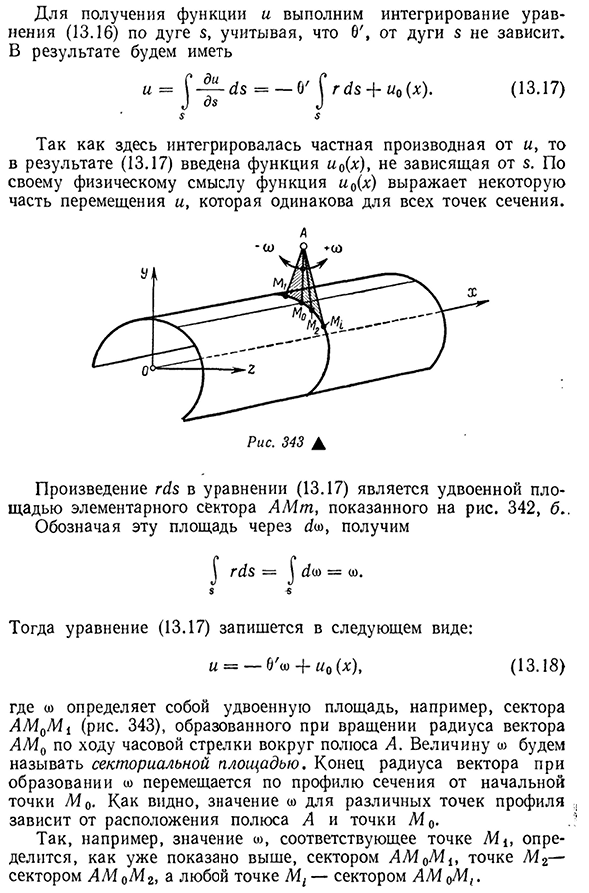
ли вы являетесь представителем данной сфере в б / унция、 gy8=Б / О)=0). Восемь. Тогда уравнение(13.17) записывается в следующем виде: I=-6\o+ » 0 (x), (13.18), где oz определяет область удвоения(например, сектор amom1). 343), образованный вращением радиуса вектора AM0 по часовой стрелке вокруг полюса A. конец радиуса вектора при образовании W перемещается вдоль профиля сечения от начальной точки M O. Так, например, значение W соответствует точке L!* , Определяется,как уже было показано выше, сектором M 0M1, точкой L42 0M2 сектором am и любой точкой 714^сектором am om,. При перемещении точки на форме поперечного сечения из точки начала координат D40 соответствующий радиус-вектор поворачивается против часовой стрелки, при взгляде на поперечное сечение в положительном направлении на ось Х 402векториальную область oz, можно определить направление формы поперечного сечения.
Поэтому для точки M1 см. рисунок. 343) W имеет отрицательный знак, а в случае точек M2 и M-C—положительный, он имеет отрицательный знак. Каждая точка в профиле W имеет свое значение и символ, поэтому она называется секторными координатами точки. Если мы возьмем частную производную функции и (13.18) x и присвоим ее уравнению (13.8), принимая во внимание, что oz не зависит от координаты x、 =- 6″О)-|-«О(х). Согласно (13.19) (13.9)и (13.19), найденным при анализе упругой деформации стержня, существует дополнительное уравнение, позволяющее., Вместе с уравнениями статики и напряжений распределения и величины
Смотрите также:

