Внецентренное действие продольной силы

Оглавление:

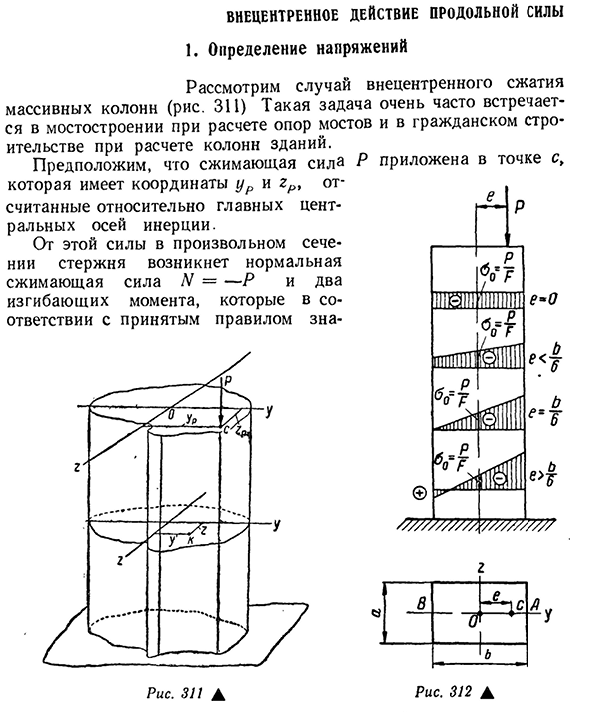
Функционирование внецентрового продольно-направленного усилия 1. Определение напряжения Рассмотрим случай сжатия в центре большой колонны(рис.311) эта проблема очень часто встречается в мостостроении в гражданском строительстве при расчете опор моста и при расчете столбов зданий. Предполагая, что сила сжатия P

приложена к точке C>, она имеет координаты ur и gr и отсчитывается относительно главной центральной оси инерции. От этой силы в любом поперечном сечении стержня возникают два изгибающих момента, которые следуют допустимым правилам обычных сил сжатия N—P и zna- Рис 312а 358 точек будут отрицательными,

так как они вызывают сжатие в точке, где они лежат в первом квартале:= — R UR> Му — РГР. Напряжение в любой точке K в положительной Людмила Фирмаль

четверти любого поперечного сечения выглядит следующим образом /V MX°=+ — C-Y+ — g-g. (11.10) в Формуле(11.10) можно найти напряжение в любой точке сжатого столбца,и для этого необходимо принять значения y и g с учетом знака. Когда один из эксцентриков равен нулю, мы теперь рассмотрим частный случай смещения центра сжатия прямоугольных колонн. Поместите силу на ось OU (g=0, y=

e), как показано на рисунке. 312 эти значения подставляются в уравнение напряжения (11.10) для получения экстремального волокна Из этого уравнения видно, что e-0 имеет одинаковое напряжение для всего сечения. Если натяжение всей секции имеет один и тот же знак(сжатие). В частности, для e= напряжения в точках A и B равны: Наконец, если e>~o~, то нейтральная ось помещается в сечение. В одном из них напряжение сжимается, а в другом-

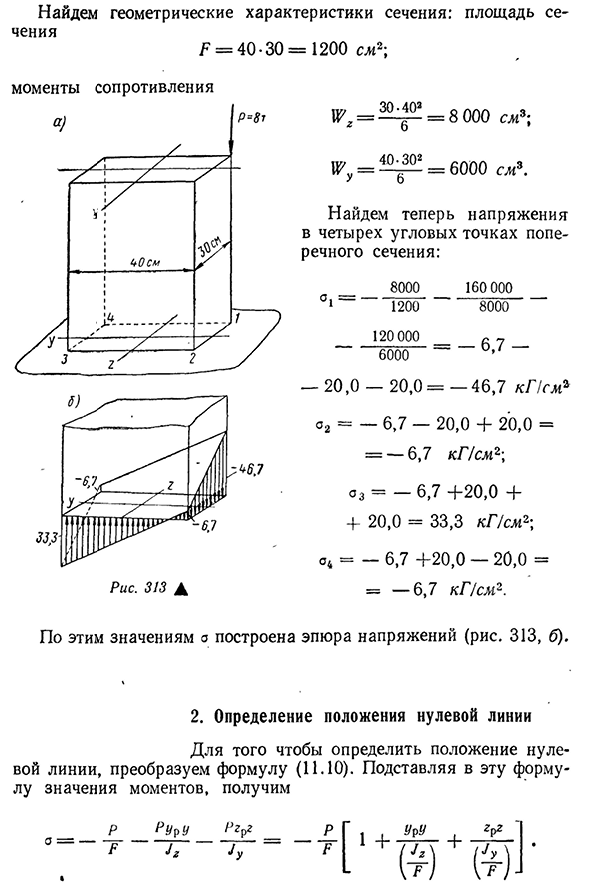
растягивается. Для этих четырех случаев на фиг. 312 показывает график напряжений. Поэтому, если вы не хотите, чтобы в сечении появлялись растягивающие напряжения, то не допускается превышение эксцентриситета. Р р и М Е Р определяют напряжения и строят их в поперечном сечении колонны(рис. 313, а). Найти изгибающий момент: Mg=+8 000-20=160000 кг\м y=+8 000-15=120000 кг-см. Сечение 359найдем геометрические характеристики: площадь сечения Г=40-30=1200EL2; ^=3 0^=8 000cm3; K’,= = 6000cm3. Теперь давайте найдем напряжение в четырех углах поперечного сечения: 8000 160 000 01-1200 8000 Сто двадцать тысяч 6000. -20,0-20,0=-46,7

КПСМ * О2= — 6,7 — 20,0 + 20,0 = = — 6,7 кг / см2 унций= — 6,7 +20,0 + + 20,0 = 33,3 кг / см2 / С4= — 6,7 +20,0 — 20,0 = = — 6,7 кг / см2. В соответствии с этими ценностями, участок стресс построена(рис. 313, б). 2. Определение положения нулевой линии Преобразуйте формулу (11.10) для определения положения нулевой линии. Если присвоить этому выражению значение момента, то получится следующее выражение 360величины стоят в знаменателе второго и третьего слагаемых, то есть квадрата радиуса инерции сечения. ■

По этой причине, (11.12) Эта формула, как и Формула (11.10), может быть использована для определения напряжений в любой точке Людмила Фирмаль

поперечного сечения колонны. Обозначим координаты любой точки нулевой линии UY, примем во внимание, что эти координаты присваиваются формуле (11.12), а напряжение в точке нулевой линии равно нулю, P Вырезать после величины -?■Получить. Уравнение нулевой линии 1++ — ^y — =0. (11.13)с Это уравнение можно использовать для определения отрезков, вырезанных нулевой линией на осях. Эти сегменты показаны. 314, а) через AU и A2. Если мы положим=0, UY-AU, то получим из уравнения (11.13 1+ Аналогично, если y^ — 0, 1-4 С. Около = 0 _ = АГ. =0. 361 если мы решим эти уравнения, то получим отрезок, отрезанный нейтральной линией на координатных осях: * 2-2 Л у= ——— 7 — : = (11.14) УР Г Р Р В то же время

можно решить обратную задачу, выразив координаты точек приложения силы P для заданного отрезка, разрезанного нулевой линией на координатных осях., (1 1л5 ) Отметим интересную зависимость величины Ur и AU, а также gr и A2,если сила приложена в точках координат AU и A2, то нулевая линия занимает нулевую линию с отрезком 314 на координатной оси, Б), а соответствующая нулевая линия занимает позицию I-/с силой, помещенной в точке 2, а нулевая линия с отрезком 314 на координатной оси Теперь рассмотрим некоторые характерные особенности, связанные с

поведением нулевой линии при различных положениях силы P(рис. 315) ось когда сила P приложена в точке на OU, нулевая линия отрезается с отрезками оси Og, равными Бесконечности: Это означает, что нулевая линия будет параллельна оси ОГ. Представьте, что сила P движется вдоль оси OU от центра тяжести к краю сечения. В этом случае нулевая линия движется от Бесконечности к сечению и всегда поддерживается параллельно оси Og. Точно так же, когда сила

движется вдоль оси Og, нулевая линия движется поступательно, и все время становится параллельной оси OU, поэтому, например, сила последовательно находится в точках 1, 2, 3, 4 (315), а нулевая линия занимает такие позиции, как I—I, II-II, ii-III, IV-IV соответственно. Рассмотрим случай, когда сила P движется по прямой OE, проходящей через центроид сечения, но не совпадает ни с одной из главных осей инерции. В этом случае нулевая линия (см. рис.315) также движется параллельно самой себе. Фактически из уравнения (11.14) вытекает следующая зависимость W V — • • 362 отсюда можно сделать вывод, что касательная наклона нулевой линии не зависит от численного значения координат точки г Это зависит от приложения сил и их

соотношения. Рассмотрим еще одну проблему, которая очень важна в дальнейших выводах. Перенести силу P Около ОДИН Ноль. 12 3Б ] 11-1. Рис ком. 315а В некоторых прямых линиях АВ не проходит центроиды сечения(рис. 316). Для двух крайних случаев, когда сила приложена к точке A и точке B, нулевая линия параллельна соответствующим осям Og и Oh. Поскольку эта точка принадлежит двум нулевым линиям, напряжение от двух сил, приложенных одновременно в точке А и точке В, равно нулю. Эта сила может быть разложена на две параллельные составляющие Rd и RV, приложенные к точкам A и B. Из этих двух составляющих, следовательно, из их результатов

напряжение в точке O становится равным нулю. Так как точка С была взята произвольно, то при любом положении силы р на линии АВ напряжение в точке О равно нулю. Исходя из этого, можно сделать вывод, что при движении груза по прямой АВ нулевая линия вращается вокруг точки О. Выводы, полученные в этом пункте, используются при последующем анализе смещения центра сжатия колонны для поведения нулевой линии, связанной с перемещением сжимающих сил по поперечному сечению.

Смотрите также:

Учебник по сопротивлению материалов: сопромату

Косой изгиб	Ядро сечения
Одновременное действие изгиба и продольной силы	Расчет на удар при изгибе