Оглавление:






Расчет бесконечно длинной балки, лежащей на сплошном упругом основании при действии на нее одной сосредоточенной силы р
- Расчет бесконечно длинных балок, Твердое эластичное основание находится в^ Под действием этого одного Сосредоточенные силы Р Рассмотрим случай, когда на бесконечную длину пучка воздействует один фокус R. это предположение позволяет использовать дифференциальные уравнения намотки^производного изгиба
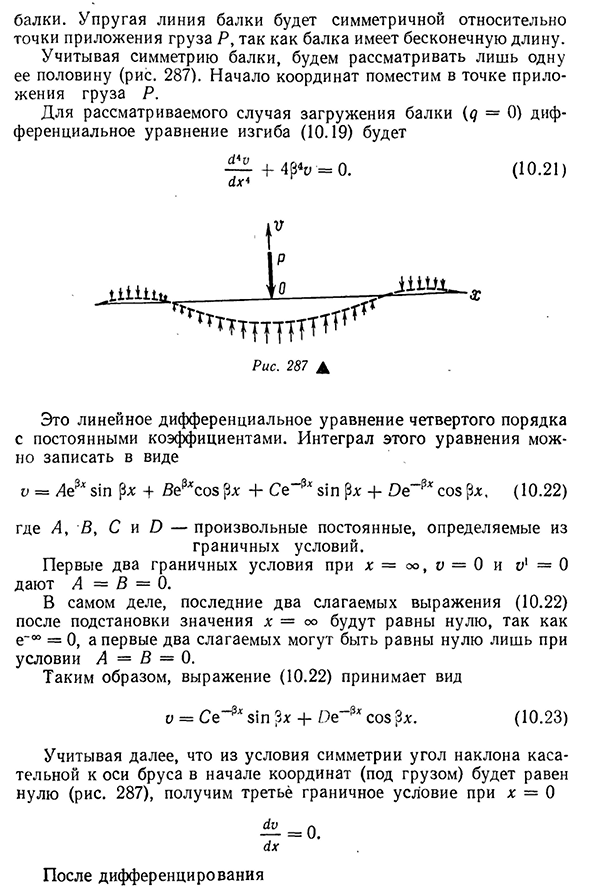
Упругая линия балки 328balki симметрична относительно точки приложения нагрузки P, так как балка имеет бесконечную длину. Учитывая симметрию луча, рассмотрим только его половину(рис. 287). Начало координат находится в точке приложения нагрузки P. Для нагрузки балки (d=0) дифференциальное уравнение для изгиба (10.19) равно—+4^=0. (10.21) Да* Г С Н Я Я_ 15———— .W-CL-D
Рис 287А Это линейное дифференциальное уравнение четвертого порядка с Людмила Фирмаль
постоянным коэффициентом. Может ли Интеграл этого уравнения быть записан как V=AE?h81p Н4-ве$^поп RH4-СЭ — $h81p{Zh4th -?Где A, B, C и y-произвольные константы, определяемые из граничных условий. Первые два граничных условия для X=OO, V-0 и Y1=0 дают A=B=0. Фактически, после подстановки двух последних членов (10.22) значение выражения x=OO будет равно нулю, поскольку e-°° ° =0, а первые два
члена могут быть равны нулю только в том случае, если a=B-0. Таким образом, уравнение(10.22) принимает форму V-СЕ-ПВ-81p ZX4th-^х поп$х (10.23) из симметрии условие 287), где угол наклона касательной касательная касательная касательной к оси координат (под нагрузкой) пучка равна нулю, а третье граничное условие Х=0 ±•=0.
- <1х Пост-дифференциация 329— = с (- ре?h8T [4-опять?x pops RH) 4-й (- re ZX POPs RH — — Заново®х ССР) И мы получаем O=C (0 4-p) 4 -/) (—P+0), или C-O выполнение третьего граничного условия. Выражение (10.23)принимает вид V=Se∈x(zsh px-px). (10.24) Рис 288А Чтобы определить четвертую произвольную постоянную, вырежьте два бесконечно близких участка балки в месте приложения силы Р(рис. 288). Принимая во внимание это сечение пучка в равновесии и принимая во внимание симметрию пучка, получаем четвертое граничное условие: x=0 Два. Если вы непрерывно дифференцируем
уравнение (10.24), вы получаете следующее: (ЗШ RH4-Попс РЗ) 4-й Ж. (Соз резус-ЗШ ОВ)]== — 2sre?h81P резус;O11= — 2sr2 (- е Zh81p резус+Е Ж поп РЗ) — = — 2sre2e?х (Соз резус-ЗШ ОВ);= — 2srz| — e_3x(Соз резус-ЗШ РЗ) 4-У,≥Х(—ЗШ резус-Соз Р х)]==4srze_?Королевское Высочество; В 4xr4 (- Е-3-кратным поп РЗ-э » 3х ЗШ резус)- — — 434[Se_3h(ZRH4-ЗШ резус)], Или ==- 4P4V. Четвертая производная от О берется для проверки правильности Интеграла дифференциального уравнения
(10.22). (10.21). Если i1u и V подставляются в уравнение(10.21), то-434y±4p4o=0. 330 это означает, что интеграл(10.22) удовлетворяет Людмила Фирмаль
дифференциальному уравнению (10.21). Если присвоить выражению значение K=0 и учесть четвертое граничное условие, то оно выглядит так Откуда После= R8rze/’ Подставляя полученное значение в уравнение дифференцирования, принимая во внимание E^n=M и E^P1=0, V= — — — — — — — e?ч(Z Т RH4-поп-8ч) — ——— тг 8r3ya / 1 ‘ 8r3e/’ _ ±_e -?x4r2e / 81P RH= П 4r2e / э?ч (соз резус-z1p РЗ)=~Т^; Для гиперболических тригонометрических функций, по формуле t]2, t] 3 Т]=e_3x(Соз резус Ф-ЗШ ОВ); Т / 1=У,√Х(Соз резус-ЗШ ОВ); Т]2=у,!3х поп РЗ;=e_3x81p резус (10.25)) Таблица (таблица) часто используемых значений аргумента px. 10). После определения значения функции t) для правой половины различных участков участка v, M и балки, t]1, t]2, t] 3. Графики V и M
по отношению к началу координат. При определении коэффициента Р коэффициент К ‘ для почв средней плотности составляет 0,5-5 кг/см3,для почв высокой плотности-5-10 кг/см3, для очень плотных почв-10-20 кг / см3. Общий вид участка М с линией прогиба V и<2 для бесконечно длинной балки, лежащей на твердом упругом основании, показан на рисунке. Двести восемьдесят девять 331T АВ л я с А10 т]=е$х (√Соз х+81PY3-г);^1=Е^(С О З^х-81prh); Т)2=е Соз?х;Т)3rd81P(1х. Долгий путь х * 11 (ВИГ 0,0 1,0000 0,0000 1,0000 1,000,000 0,1 0,9907
0,0903 0,8100 0,900 0,1 0.2. 0.9651. 0.1627. 0.6398. 0.8024. 0.2. О, З0.,9267 0,2189 0,4888 0,7077 0,3 0,4 0,8784 0,2610 0,3564 0,6174 0,4 0.5 0.8231 0.2908 0.2415 0.5323 0.5 0,6 0,7628 0,3099 0,1431 0,45 0,6 0,7 0,6997 0,3199 0,0599 0,3708 0,7 1 / 4Л: 0,6448 0,3224 0,0000 0,3224 0,785 0,8 0,6354 0,3223 -0,0093 0,3131 0,8 0,9 0,5712 0,3185-0.0657 0,2527 0,9 1,0 0,5083 0,3096-0,1108 0,1988 1,0 .1,1 0,4476 0,2967-0,1457 0,1510 1,1 1,2 0,3899 0,2807-0,1716 0,1091 1,2 1,3 0,3355 0,2626-0,1897 0,0729 1,3 1,4 0,2849 0,2430-0,2011 0,0419 1,4 1,5 0,2384 0,2226-0,2068 0,0158 1,5 1 / 2l0,2079 0,2079 — 0,2079 0,0000 1,571 1,6 0,1959 0,2018 -0,2077 -0,0059 1,6 1,7 0,1576 0,1812-0,2047-0,0235 1,7 1,8 0,1234 0,1610-0,1985-0,0376 1,8 1,9 0,0932 0,1415 — 0,1899 -0,0484 1,9 2,0 0,0667 0,1231-0,1794-0,0563 2,0 2,1 0,0439 0,1057-0,1675-0,0618 2,1 2,2 0,0244
0,0896-0,1548-0,0652 2,2 2,3 0,0080 0,0748-0,1416-0,0668 2,3 3 / 4tg0,0000 0,0670 -0,1340 -0,0670 2,356 2,4 -0,0056 0,0613 -0,1282 -0,0669 2,4 2,5-0,0166 0,041-0,1149-0,0658 2,5 2,6-0.0254 0,0383-0.1019-0,06,2,6 2,7-0,0320 0,0287-0,0895-0,0608 2,7 2,8-0,0369 0,0204-0,0777-0,0573 2,8 2,9-0,0403 0,0132-0,0666-0,0534 2,9 3,0-0,04226 0,00703-0,05632-0,04929 3,0 3,1-0,04314 0,00187-0,04688-0,04501 3,1 Т.: -0,04321 0,00000 -0,04321 -0,04321 3,142 3,2 -0,04307 -0,00238 -0,03831 -0,04069 3,2 Z,я-0,04224 -0,00582 -0,03060 -0,03642 3,3 3,4 -0,04079 -0,00853 -0,02374 -0,03227 3,4 3,5-0,03887-0,01059-0,01769-0,028,5 3,6-0,03659-0,01209-0,01241-0,02450 3,6 — 3,7 -0,03407 -0,01310 -0,00787 -0,02097 3,7 3,8-0,03138-0,01369-0.00401-0,01770 3,8 3,9-0,02862-
0,01392-0,00077-0,01469 3,9 5 / 4Л-0,02786 -0,01393 0,00000 -0,01393 3,927 4,0 -0,02583 -0,01386 0,00189 -0,01197 4,0 4,1-0,02309-0,01356 0,00403-0,00953 4,1 4,2-0,02042-0,01307 0,00572-0,00735 4,2 332prodolzhenie ST) g-4wwith Yu g St04>00 00^ — 400with04on 04 4^ — 4o Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh Oh 10г 0-У^-ч оо)оо)0o0o ssoo0ch0-<МО г ооочень-ооочень оо оо оо оо о оо о оо о оо о оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо оо г-ну O04 00 00so ю о о о так.О-nsoyu04o о U г-. Г-т± » O04 04 04t-<о 00 04 04o so04so<О О 00 г o04Yo SO00-так Yu04 04 г-Ю так O00g-ю SO04o о о
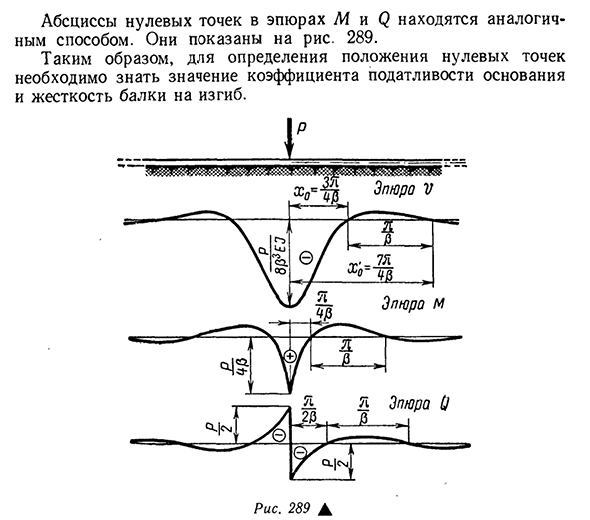
о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’о’ II I к 1CP II II К Я О Я О S СР Отчет О! К д Я х—» б О, Я. I o S К Б Аналогичным образом найдены абсциссы нулевых точек графиков M и f. Они показаны на рисунке. Двести восемьдесят девять Поэтому для определения положения нулевой точки необходимо знать коэффициент податливости основания и величину жесткости изгибаемой балки.
Смотрите также:

