Оглавление:






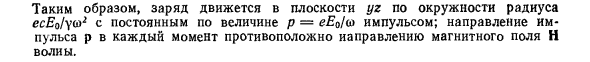

Монохроматическая плоская волна
- Монохроматическая плоская волна. Важный частный случай электромагнитных волн представ .. Ляют волны, в которых поле является простой периодической функцией времени Такая волна называется монохроматической
Все величины (потенциалы, компоненты полей) в монохроматической волне зависят от времени посредством множителя вида соз (сot + се), где оо — циклическая частота (или просто частота ) волны. В волновом уравнении вторая производная от поля по време теперь будет д2 f / dt2 = -uo2f А / + Ј / = О- (48,1) В плоской волне Поэтому если плоская .
Векторный потенциал такой волны удобнее всего написать в виде вещественной части Людмила Фирмаль
Волна монохроматична, то ее поле является простой периодической функцией от т — х / с комплексного выражения: А = Re {А0е — «(*« х / с)}. (48.2) Здесь Ао-некоторый постоянный комплексный вектор. видно, что и напряженность (48.3) поляризованные координаты
Вектор к = -п (48,4) С (где п-единичный вектор в появлении распространения волны) называется волновым вектором. A = Re {A 0e * (kr-a, t)}, (48,5) не может быть выбрано осей координат. До тех пор, пока мы не получим отдельные операции, можно опускать знак подставив А = Аое ^ кг- ^ в (47.3), получатель связи между напряженностями и векторным потенциалом плоской монохроматической Е = икА, Н = г [кА]. (48,6)
- Рассмотрим подробнее матической волны. E = Re {Eoe * (kr- ^} (Все сказанное ниже относится, разумеется, в той же мере и к магнитному полю). Ео есть некоторый комплексный вектор. Его квадрат уравнение есть некоторое, вообще говоря, тоже комплексное число.
Если аргумент этого числа есть —2а (т. е. уравнение = | Ед | е_2га), то вектор Ь, определенный согласно Е 0 = он, (48,7) будет иметь вещественный квадрат Ь2 = | Ео | 2-С таким опреде лением напишем Е = Re {Ье ^ (кг «ш *« а)}. (48,8) Представим б в виде b = bi + гЬ2, В квадрате Ь2 = = b \ — + 2гЪ \ Ъ2 должен быть вещественной величиной, то b ib 2 = 0, т. е. используются би и взаимно перпендикулярны. тогда из (48,8м) Еу = Ъ \ cos (вырезать-кр + се), Ez = = Ь & 2 sin (сот-кр + а), (48,9)
мы видим ства вектор электрического поля вращается в плоскости Людмила Фирмаль
где знак плюс или минус направленный в положительный или отрицательный вектор прямой осью z. Из (48.9) следует, что Т? 2 Z712 f + f = 1. (48,10) b 1, b2 Таким образом, , перпендикулярной к направлению распространения волны, причем его конец описывает эллипс (48,10).
Такая волна называется эллиптически поляризованной. Вращение происходит в направлении по или против направления винта, ввинчиваемого вдоль оси ж, соответственно при знаке плюс или минус в (48,9). Если то эллипс (48.10) превращается в круг, т. вектор полярных волн очевидно, что это становится очевидным. Отметим, что в таком волне отношение у- и ^ -составляющих комплексной амплитуды Ео равно ^ = ± г (48.11)
Еру соответственно, правая и левая поляризация). Наконец-то, если Ь \ или 62 равно нулю Лено везде и всегда рядом (или антипараллельно) одному В этом случае линейно поляризованной или поляризованний поляризованную волну можно рассматривать, очевидно, как наложение двух линейно поляризованных вол Вернемся к определению рехмерный волновой вектор # = (^, к). (48.12) 4-вектор, очевидно, что при умножении на 4 волны он дает скаляр-фазу волны: kiXг = сот-кр. (48.13)
Из определений (48.4) и (48.12) видно, что квадрат волнового к% = 0. (48.14) Это выражение должно А = Ао exp (—ik (Xг) должно быть решение волнового уравнения (46.10). Как у всякой плоской волны, в монохроматической волне, распространенные по всей стране, только следующие компоненты тензора энергии-импум. rj-100 _ rj ~ l01 _ rj-ill _ уу С помощью волнового в тензорном виде как Тик = ^ -к? К к. (48.15)
Наконец, используя закон преобразования волнового 4-векто можно легко рассмотреть так называемый эффект Доплера-изменение частоты волны, испускаемостьии по отношению к наблюдателю, по сравнению с «собственной» частной речью Пусть V-скорость источника, т. Е. Скорость системы отсче та К 0 относительно К.
Согласно общей форме ислама Я 4-векторов имеем ^ (0) 0 = к0- (У / Ф1 у / 1-V 2 / с2 (скорость системы К относительно Ко есть-V). к0 = со / с, к1 = кос а = -кос се, где се —угол (в системе К) между направлением испускания волн и волнений источник, получающий ш = шоЛ Е Ш ^, (48,16) 1- (V / c) cos а У нее есть искомая формула. не слишком близок к 7г / 2: 00 L0o (l + -cosce ^. (48.17) При а = 7г / 2 имеем ш = ш0 ^ 1-и UQ (л-; (48,18) в этом случае относительное изменение частоты пропорционально квадрату отношения V / c.
Задачи 1. Определить направление и значение осей эллипса поляризации по комплексной амплитуде Ео- B = bi + с вещественным квадратом. Из (48.7) имеем EoES = bj + bl, [EoEq] = —2г [bib2], (1) ИЛИ b \ + b \ = A2 + B2, bi b2 = AB sin <5, где введены обозначения \ E0y \ = A, \ Ео, \ = В, ^ = Для абсолютных значений фаз (6) между ними. 26i, 2 = VA2 + В2 + 2ABsin6 ± л / А2 + В2-2AB sin8, (2) чем полярность поляризации.
Для определения их разрешения осей у, z) исходим из равенства R e {(Eob!) (ESb2)} = 0, в котором легко убедиться, подставив Ео = (bi + гЬ2) е ~ гос. равенство в координатах у, z, получатель и осью у (g2e = 2A B ^ (3) Направление вращения поля определено знакомыми ж-компонентами векто ра [ЬгЬг]. Написав из (1) 2i [b! B2] * = E0zE * 0y-E * 0zE0y = \ Е0у | 2 {(| ^) — (f r 1) *}. мы видим, что направлено на сторону [по-русски]
Направления осей х). правление винта, ввинчиваемой вдоль оси х) дается знакомым мнимой части отношения E oz / E oy (плюс в первом и минус во втором случае). обобщает правило (48.11) при круговой поляризации. 2. Определить движение заряда в поле плоской монохроматической линейно поляризованной волны.
Решение полярности пишет: Еу = Е = Ео, потому что Ау = А = ——- sinc <jЈ со (Ј = t-х / с). По формелам (3), (4) задачи 2 §47 находим (в системе отсчет, в какой части в среднем покоится) (параметр rj = ujЈ) представление движения: х = —— ^ sin 2т], у = ———— 5-со sf7, z = О, 87 до 7удж е 77 2 tti2 2 tti2Ь 0. 2 2 2 G Ь0 1 = «cj-8T7 ^ ~ о; 5sm211’ ‘1 = ™ ° + — ^, 2 SOC ——— = о е ^ ° • n77, Py = —— S1I177, Pz = 0. 47a; Cd
Заряд, движущийся в плоскости ЖТ / по симметричной 8 -образной кривой с про Период движения отвечает изменению параметра ра г] от 0 до 2тт. 3. Определить движение заряда в поле поляризованной волны. Решение. Е у = Ео coscjg, E z = Ео sincj ^, c cE q .. j cE q. Ay = ——— sm Az = —— coscj ^. UJ UJ
Движение определяется формулами: ecE0 есЕ0. х = 0, у = ——— cos cjЈ, z ———- smujt, 7 UJ JUJ еоо. px = 0, py = —— sm ujt, pz = ——— cos ujt, UJ UJ „2 jp2 2 2 2, С М / 0 7 = m с H —— UJ Таким образом, ccEq / ^ uj2 с постоянным по величине импульсом р = еЕо / ш \ направление магнитный импульс поля Н волны.
Смотрите также:
| Волновое уравнение в физике | Спектральное разложение |
| Плоские волны в физике | Частично поляризованный свет |

