Свойства определенного интеграла с примерами

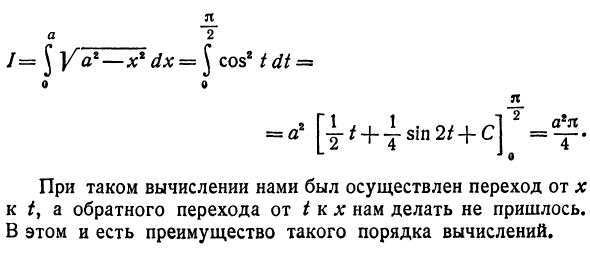
Свойства определенного интеграла

• Определенные интегральные характеристики Как показано в §3, определенный интеграл вычисляется с использованием неопределенного интеграла (т. Е. С использованием антидифференциальной функции). Поэтому гл. X, §§ 2 и 3 перенесены в определенный интеграл. У нас есть: S [/ () + Ф ()] dx = JДх) dx + JФ (x) dx, а б б J cf (x) dx = c J / (x) dx, И ах J / ()
• ()] φ ‘(x) dx, И воровство [f (x) dx = \ f (x) dx + \ f (x) dx. Уравнения (I) — (111) используются без особых затруднений, но замена переменной (IV) требует объяснения.

Это дается на примере. . в б На самом деле, интеграл дх J7 a Площадь изогнутой трапеции aABB (рис. 83), А интеграл \ f [x) dx и J / (*) dx — это площадь переменного тока Глава Получено в § 4 § 2. X, мы получаем Я / = 3 J x sin x dx = 3 [-x cos x + sin l; 4-C] * = Около 0 = 3 [—l cosl + sin i + C] -3 [0 cos 0-f sin O-f-C] -Зя. но Пример 2. / = ^ | / a2 —π * tx.

Уравнение (V) выражает характеристики конкретного интеграла, очевидные из его геометрического значения Людмила Фирмаль

Сделать то же самое изменение о Глава § 3 Pr. Используя переменную X вроде 3 и полученный там результат, O l j ° a2 .a • i a2 ^ = -77 Арксин- = -77 Арксин 1 = -. 2 a 2 4 Здесь мы переключились с переменной x на переменную t (при вычислении обратной производной) и сделали обратный переход от t к x.

• Поскольку этот пример был проанализирован ранее (гл. X, § 3, пр.3), расчет не делает этот переход. Другими словами, вы можете вычислить различными способами, подставив x = sin t (). Пересчитать пределы интеграции. g: если = 0, (), 0 = asin /, то есть sin / = 0, то f .- = 0. Если x = a}, (*) означает a-a s \ nt, sin / = 1 wherece * = • Таким образом, когда x изменяется от 0 до a, переменная t р \ 71 Это изменяется от 0 до y.

Учитывая все вышесказанное, вы можете написать:Я 2 / = 5 | / a2 — x2 dx = \ cos21 dt = Ах ах В этом расчете был выполнен переход от x к t, но обратный переход от t к x не является необходимым. Это преимущество этого порядка расчета.

В уравнении (IV) числа a и p являются значениями переменной x. Людмила Фирмаль

Соответствует значениям a и b в переменной z. я 2 C cos x Пример 3. Вычислить интеграл 1 = \ ^ _ ^ sin2 ^ dx. Здесь, 0 / = sin; установите c () для изменения переменных. Отсюда L Излучение: если x = 0 / = 0 и если l; = — / = 1. производная (), dt = cos x dx, следовательно, I 2 1

Смотрите также:

Предмет высшая математика

Определенный интеграл	Задачи на применение определенного интеграла
Вычисление определенного интеграла при помощи первообразной функции	Площадь криволинейной трапеции