Оглавление:



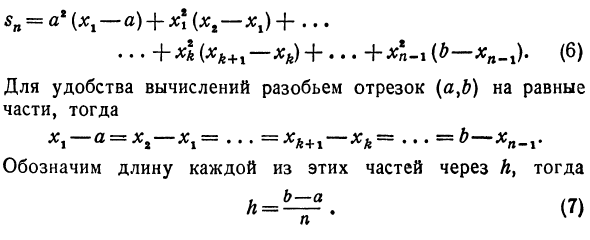

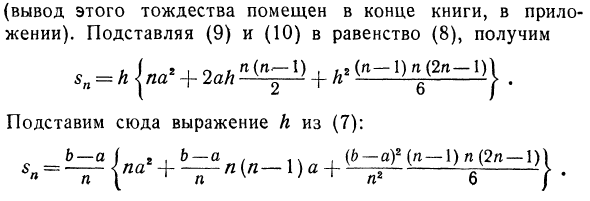



Приближенное вычисление площадей криволинейных трапеций
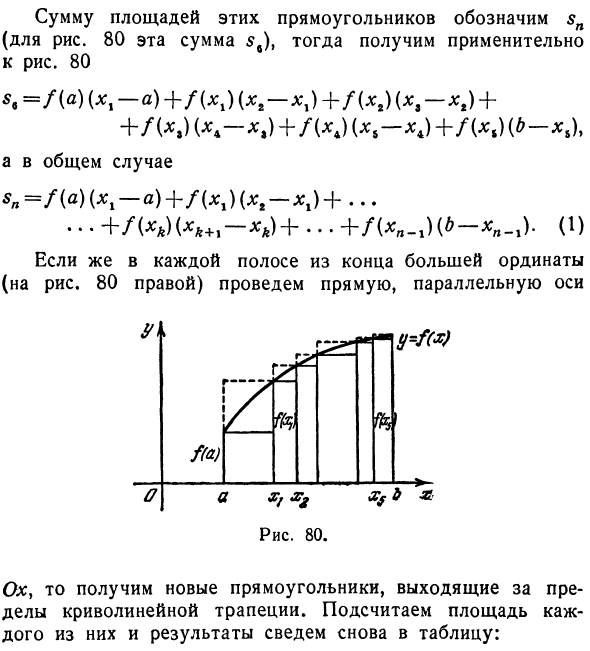
- Приблизительный расчет изогнутой области трапеции Глава 4 в IX. Дано определение изогнутой трапеции. В этом разделе определите хотя бы приблизительную площадь. Рассмотрим изогнутую трапецию, окруженную кривой y = f (: c), осью Ox, прямой линией x = a и x = b (рис. 80). Сегмент (a, b) делится на n частей в точках x1Y x2, x9> xk> •••> xn-1 (рисунок / 2 = 6), и из этих точек ордината yk = f (xk) восстановить. Построенная ордината делит трапецию на n полос (6 полос на рисунке).
80). Таким образом, вы получите n прямоугольников (на рисунке 80 6 прямоугольников). Рассчитайте каждую область и сведите в таблицу результаты. Прямоугольная высота основания 1-a f (a) (Xl-a) 2 xg-x, / ш 3 xz-x2 / ()) f (xt) (x9-xg) 4 Xt — Xt / (,) f (Xt) (xA-xt) 5 / (* ) f M (, — * 4) 6 b-xb ft *. ) Нет. )
Нарисуйте прямую линию, параллельную оси Ох, с каждой полосой от конца маленькой ординаты (левая сторона рисунка Людмила Фирмаль
Общая площадь этих прямоугольников обозначена $ n (на рисунке 80 эта сумма равна se). 80 s9 = / (a) (xl-a) + / (xl) (x1-xl) + f (xi) (x9 ^ xt) + + / (.) + + / ( ■) Y — ), Но в общем случае sn = f (a) (x1-a) + f (xl) (xt-x1) + … ••• + / () (** +, — *) + •••• + / ( ”-”) (* — *, «-») • 0) При рисовании прямой линии, параллельной оси, с каждой полосой от конца большой ординаты (правая сторона рисунка 80) О, а затем возьмите новый прямоугольник над изогнутой трапецией. Рассчитайте каждую область и верните результаты в таблицу.
СП «Площадь прямоугольной высоты основания 1-a / (,) / ( l) (! — C) 2 X2 — Xx /(.)/(pass) |) 3 рт.ст. и * «) / (*») * 2) 4 / (* 4> 5 * 4 / <. ) F ( $) (^ 5- ^ 4) 6 b — xb 1 (b) 1 (b) (b-xb) Если общая площадь этих прямоугольников представлена SnJ, она будет применена к рисунку 1. 80 + f (x>) (xg-xA) + f (b) {b-xt), Но в общем случае $. = / (* ») (Xi-a) + / (x2) (xa-xi) + … ••• + / (** +.) (** + ”- *) + ••• + / () Φ— xn-x) (2) Если область изогнутой трапеции обозначена буквой Sy, получается очевидное неравенство sn <S <Sn. (3) Поэтому, если вы возьмете Sn на 5, приблизительное значение области 5 будет чрезмерным, а если вы возьмете Sn на S, этого будет недостаточно.
- Это написано как: (4) (5) 5. Приблизительные значения областей sn и Sn различаются на Sn — sn. Пример 1. Найти приблизительную площадь изогнутой трапеции Парабола y = xr, ось x, прямая линия x — a и x = b (рис. 81). Почти равно (5). Когда sn рассчитывается по уравнению (1),”=“ In (* 1- ”) + * J (* t— * l) + ••• • .. + xCxk + r-Xk) + … + X * n-x (b-Xn_x). (6) Для удобства расчета разделите сегмент (айб) на равные части, xi a = x8 xl = … = xk + l xk = … = b xn_x. Длина каждой из этих частей обозначена буквой А, , Б — а
В этом случае вы получите: Xjsa + ft, xt = a — \ — 2h, xs-a-f-ZL, … …, хк-а + …, б = а + ти.h) 2ч Или скобка ч sn = h {a1 + (a + h) t + … + (a + kh) * + … … + [in + (l_1) h] 2}. Если вы откроете небольшую скобку, sn ^ h {a2 + a2 + 2ah + h2 +. , , + а * + 2ах + к2х2 + … .. + a3 + 2a (n- ) h + (n-l) 2h2}. Сократите эти термины в фигурных скобках, выньте 2ah и A2 из скобок, sn = h {pa2 + 2ah [I + 2 + … + k +. .. + (l-1)] + + A «[l + 2» + … + ft «+ … + (* -!) ‘]}. (8) Пусть выражение результата будет в более простой форме. По этой причине обратите внимание на следующее: 1 + 2 + … + * + … + (* -!) = 2-2 (как сумма членов арифметических рядов) и I2 + 22 + … + £ 2 +. .. + (/ r-1) 2 = n (2n-1) (10)
Уравнение (6) можно записать в следующем виде: = aH + (a + A) f h + … + (a + kh) 2 h +. .. … + [a + (α- ) Людмила Фирмаль
(Вывод этой личности дается в конце книги приложения). Подставляя (9) и (10) в уравнение (8), -И {яд ‘+ 2ahg- + L’ ‘U * «. Здесь подставим выражение h в (7). Б — а я г. Б — а. 1 час (б-а) 2 (н-я) л (2л-1))Положите ~ в фигурные скобки, чтобы уменьшить его. , = (* — «) {A ‘+ (* «) «= 1 a + (* «) ■, 1-1) (I) Если уравнение (4) используется для приблизительного расчета площади »S, а уравнение (2) используется для расчета Sn, то используется совершенно аналогичный расчет: + (»-«) • (l | + l) (4- + l)}. (12) Желаемая площадь 5 изогнутой трапеции составляет от 5 до 5. То есть sn — a3 (B — a) | a2 -) — (^ —a) a +
Предел в правой части (12) уравнения также равен — ^ -. Используя эти длинные вычисления, мы подтвердили, что и sn, и Sn имеют тенденцию быть одним и тем же пределом при дроблении сегментов сегментов (a, b). Так что в случае н-йо, 5 между ними,
Смотрите также:
| Преобразования неопределенных интегралов | Определенный интеграл |
| Замена переменного интегрирования (метод подстановки) | Вычисление определенного интеграла при помощи первообразной функции |

