Оглавление:




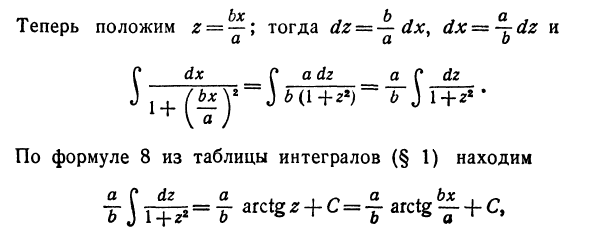


Замена переменного интегрирования (метод подстановки)
- Замена переменной интеграции (метод замены) В этом разделе мы рассмотрим преобразование интеграции в другую форму. Это может оказаться более удобным. Если задан интеграл ^ f (z) dz, то z — это функция x: z = cp (x :), и верно следующее выражение: $ / (* M * = $ / [<Р () 1Ф ‘() Л . (IV) Это называется выражением подстановки интеграции переменных. Проверьте с помощью дифференциации.
Применяя формулу (B) в § 1, d \ f (z) dz = f (z) dz () z = <$ (x) dz = f ‘(l 🙂 dx. Подставляя полученное выражение в уравнение (), ) & = / [φ (: 🙂 1ф ‘(x) dx. . Следовательно, обе стороны уравнения (IV) могут различаться только постоянным членом, что означает, что уравнение (IV) верно.
Нахождение производной в правой части уравнения (IV) приводит к тому же уравнению Людмила Фирмаль
Пример 1. ^ sin1 l; cos * put z = sin. ; Тогда dz = cos x dx. Присвойте данному интегралу ^ sin8 xcosx dx = = \ z9 dz. Применяя уравнение Γ из таблицы интегрирования, J sin’l: cos x dx = ^ zldz + Пример 2.x2xdx. a1 — устанавливает x1 = zt (). Тогда xj = a1 — zty 2 xdx = -2 zdz или xdx — zdz. так j Ya * —x2 xdx = ^ z {—zdz) = — ^ zl dz = -j + C Чтобы вернуться к старой переменной x>, найдите z из уравнения (*). z = Ya * — наконец 8 j Y ^ r ^ x dx = — (~ 3xi) 1 + s Пример 3. J Va ‘- xi dx. Рассмотрим интеграл перед преобразованием этого интеграла J cos * / dt.
Примените выражение к косинусу полуширины cos = = 1 + cosa и положить = 2 / в нем. Тогда cosl / = 1 + cos 21 = 2 = + J dt + j§cos2tdt. J cos 2t =; легко понять. Это можно легко подтвердить, сделав различие. так cos1 / L = i / + t Sin 2 / + C (*) £ cos * / ctf = J * dt и целое
- Вернуться к интеграции J Vag-x1 dx. х ~ син т (), V a1 — x2 = Va * -a * sin * t = a cos t и dx = стоимость dt. При использовании (*), j a2-x2 dx = a1 J cos * t dt = a1 [1 / + jsin 2 / + c] = = ~ + Sin t cos t + 2cj # Здесь мы возвращаемся из уравнения () к переменной x . х С / «» «* Г х / = arcsin ~ и, следовательно, \ y a * -xd dx = — ^ — arcsin- + + ~ J / ~ l- + CJ9, где Cx — любая постоянная. Пример 4. J f (x). Положим z = <p (x), затем дз = у ‘(х) дх. Следовательно, j * dx = J ~ = В z + C (в таблице интегрирования нет уравнения 2). Вот так Пример 5. ^ fl2 ^ b2x2 ‘Сделайте некоторые преобразования Ваня: Использовать dx_D Использовать dx__J_ dx Где z- \, dz = -dx, dx = ^ rdz, 9 б D dx __ D adz a C DZ l + * e ‘ J 1+ (-Y J 6 Oh J + ш Найдите Сdz a из таблицы интегрирования (§1), используя уравнение 8. а, бх, ~ Y J + 7> = Y arctg * + C = Tarctg- + C,
Таким образом, D dx 1 a l bx. ~ 1, бх, „ \ =? T arctS T + C = 5F arct «T + C- Этот курс ограничит вас этими примерами, но имейте в виду, что вы можете бесконечно увеличивать количество примеров и показывать тип интеграции, который приобретается или рассчитывается определенным образом. Это сделано с более полным курсом.
Смотрите также:
| Первообразная и неопределенный интеграл | Приближенное вычисление площадей криволинейных трапеций |
| Преобразования неопределенных интегралов | Определенный интеграл |

