Обратное дифференцирование и неопределенный интеграл

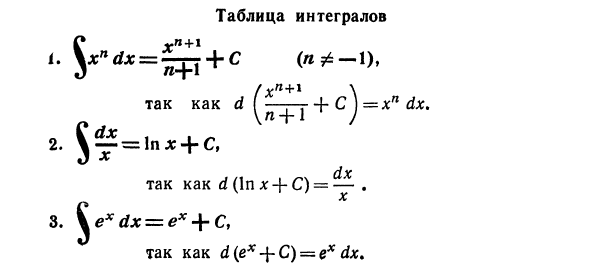
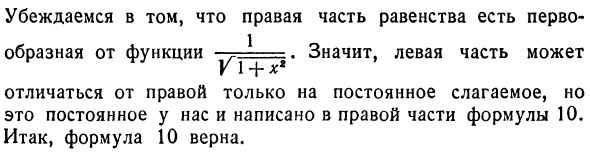
Первообразная и неопределенный интеграл

• Обратное дифференцирование и неопределенный интеграл Определение. Обратной производной данной функции / (*) является функция F (x), производная которой f (x) dx}. Другими словами, dF (x) = f (x) dx. Например, функция xx является обратной производной функции Zl. 1 потому что дх * = 3х * дх. Площадь F (x) кривой трапеции (Ch, согласно IX § 4) является обратной производной функции f (l :), и ее график ограничивает эту кривую трапеции. dF (x) = f (x) dx. Пример 1. Указывает, что функция arctgx является обратной производной функции. На самом деле, производные Я * * г * arctg * равно , R, следовательно, разница 1 ‘x 1 т xi дх.

Следовательно, arctg * является обратной производной от Определение антидериватива может быть дано в другой эквивалентной форме. Обратите внимание, что обратная производная этой функции не существует сама по себе. Например, как указывалось, x9 является обратной производной от 3jc *, но принимая функцию x ‘+ C (C — любая постоянная), d (x * -C) = 3: * * dx> т.е. xg -f C также является обратной производной от xxg. Вы можете доказать, что противоположное предложение также верно.

Антипроизводным функции f (x) является функция F (x) y с производной f (x). Людмила Фирмаль

То есть, если функции Fx (x) и F2 (x) являются обратными производными функции f (x), они отличаются друг от друга Друзья на определенный период. При этом операция нахождения антидериватива является, во-первых, операцией, противоположной дифференцированию, и, во-вторых, эта операция неоднозначна, то есть в результате ее применения различные операции изменяются в зависимости от постоянного члена.

Функция получается. Определение Множество всех обратных производных определенной функции называется неопределенным интегралом этой функции. $ / () Dx = F (x) + C Неопределенный интеграл показан как: \ ^ f (x) dx, а чтение: неопределенный интеграл от функции f (x). Если F (x) является одной из обратных производных функции f (x), любая другая обратная производная той же функции равна (А) Из определения примитивного и неопределенного интеграла, d [f (x) dx = d [F (x) + C \ = dF (x) + dC = dF () = / (*) dx. Напишите выражение, которое проверяется дифференцированием.

• Интеграционный стол / xn + x \ d- + C) — после xn V ^ + л / — = ln x + C, X 1 дх Потому что d (In x + C) = -. ex dx = ex + C, Потому что d (ex-J-C) = ex dx.^ cos xdx = s \ n + C, d (sin x + C) »из cos x dx. б. ^ sin x dx = -cos jc -J- C, Потому что d (-cos * + C) = sinxdx. с. = tg * + C, 3 cos1 l: e 1 Потому что d (tgx + C) = —r потому что * X 7. Если df = -ctg x 4-C, 3 sin2 X в -G Из ctg q: + C) = ^^ 8-§rqpr ^ = arctg * + Cf дх рф (арктан х с) = дх 9. V _ = = arcsln x + C, Из d (арксин d: + C) , 0- STTTS ^ 1 » Проверьте уравнение 10. Взяв производную от левой части уравнения, получаем [по уравнению (B)].

Поэтому мы уверены, что левая часть является обратной производной функции -y. Возьми разницу сейчас 10 с правой стороны равенства: d \ n (x + Y \ + x2) = [\ n (x + / T + 7)] ‘(/ a: = , _ = (1 + *) dx = X + YT + 74_V \ + W 1 Вл + х2 + хдх == д * x + y \ + xy yT + 7 * Vi + 1 Я уверен, что правая часть уравнения является обратной производной функции y. Так что левая сторона Только постоянный член отличается от правой части, но эта постоянная описана в правой части уравнения 10. Следовательно, уравнение 10 является правильным.

Смотрите также:

Предмет высшая математика

Применение к приближенным вычислениям	Преобразования неопределенных интегралов
Применение дифференциала к различным задачам	Замена переменного интегрирования (метод подстановки)