Исследование функций на возрастание и убывание

Исследование функций на возрастание и убывание

• Увеличение / уменьшение функции исследования Вышесказанное позволяет изучать возрастающие и убывающие функции. Вот пример: Пример 1. Рассмотрим функцию y = 2x * -3 * 1-12l: -6. Чтобы узнать, где эта функция увеличивается и где она уменьшается, вам нужно определить, где производная положительна, а где отрицательна. Поскольку изменение символа возможно только при прохождении важных значений, вы должны сначала найти эти значения. Найдите производную: y ‘= 6x * -6x — 12.

• Критическое значение — это значение, при котором производная исчезает. уравнивание При решении производной до нуля полученное уравнение находит критическое значение: = –1, x2 = 2.

Нет другого критического значения, потому что производная везде. Людмила Фирмаль

Таким образом, дифференцирование может изменить знак, только если независимая переменная проходит через x1 = -1 и x2 = 2. Эти значения делят ось X на три секции. 1) -оо <* <-1, 2) -1 <* <2 3) 2 <х <+ оо. Если вы изменяете независимую переменную в каждом из этих разделов, производная сохраняет свой знак (в противном случае он должен снова быть нулевым, но не таким).

Примите любое значение x, чтобы узнать, какой знак имеет производная в рассматриваемом разделе. Найдите знак производной, которая принадлежит этому разделу и имеет это значение х. Так, например, раздел —oo 0. Если сечение- \ , число η = Получите 10 и получите f ‘(10) = 600–60–12> 0.

• Поэтому, если вы измените l, см. § 1 этой главы, потому что производная от -оо до -1 положительна. При изменении x от -1 до 2 функция уменьшается, поскольку производная становится отрицательной. И, наконец, когда n: изменяется от 2 до oo, производная становится положительной, то есть функция увеличивается (рисунок 54). Результаты исследования сведены в таблицу.

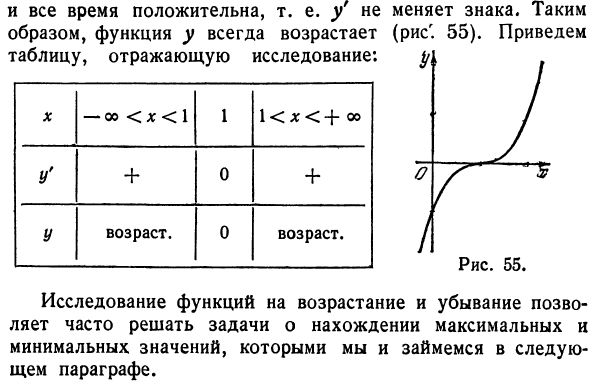
Всегда положительный, т. Е. У не меняет знак. Поэтому функция y всегда увеличивается (рисунок 55). Таблица, отражающая это исследование, выглядит следующим образом. Рисунок 55. Х-оо <х <\ 1 \ <х <+ оо Y ‘+ 0 +

Производная y ‘= 3 (x-1) 2 исчезает только тогда, когда η = 1. Людмила Фирмаль

Есть возраст. 0 лет Изучая функции увеличения и уменьшения, вы часто можете решить проблему нахождения максимальных и минимальных значений. Это описано в следующем разделе.Х-00 <х <- \ — 1-1 <х <2 2 2 <х <+ оо Y ‘+ 0-0 + Есть возраст. 1 вниз — 26 лет. Пример 2. Рассмотрим функцию y- (x-1) *.

Смотрите также:

Предмет высшая математика

Вторая производная. Производные высших порядков	Максимальные и минимальные значения функции
Возрастание и убывание функции	Выпуклость и вогнутость линии. Точка перегиба