Оглавление:



Статически неопределимые балки при изгибе и метод их решения
- Статически неопределенные балки В способе изгиба и его определении Метод определения смещения, описанный в предыдущей главе, широко используется при расчете так называемых статических неопределенных Пучков / расчетах сложных статических неопределенных систем более подробно » механизм в этой главе мы
рассмотрим, как вычислить простейшие статически неопределенные пучки. Балка, способная принимать любую нагрузку, должна быть закреплена так, чтобы она не могла двигаться как твердое тело. В случае действия нагрузки в одной плоскости минимальное количество соединений, необходимых для фиксации балки,
равно трем. Эти три соединения абсолютно необходимы. Удаление хотя бы Людмила Фирмаль
одного из этих звеньев превращает балку в геометрически изменяемую систему (механизм), то есть точку можно перемещать без деформации стержня. Поскольку три уравнения равновесия могут быть построены для плоской системы сил, то реакция абсолютно необходимой связи может быть получена только с помощью статического уравнения. Балка, фиксируемая такими связями,
статически определима. На практике встречаются балки с большим количеством соединений, наложенных больше, чем необходимо для обеспечения геометрической устойчивости* 304 в этом смысле некоторые связи являются «лишними». В пучке с избыточной связью все реакции не могут быть определены только из уравнения равновесия. Такой луч становится статически неопределенным.
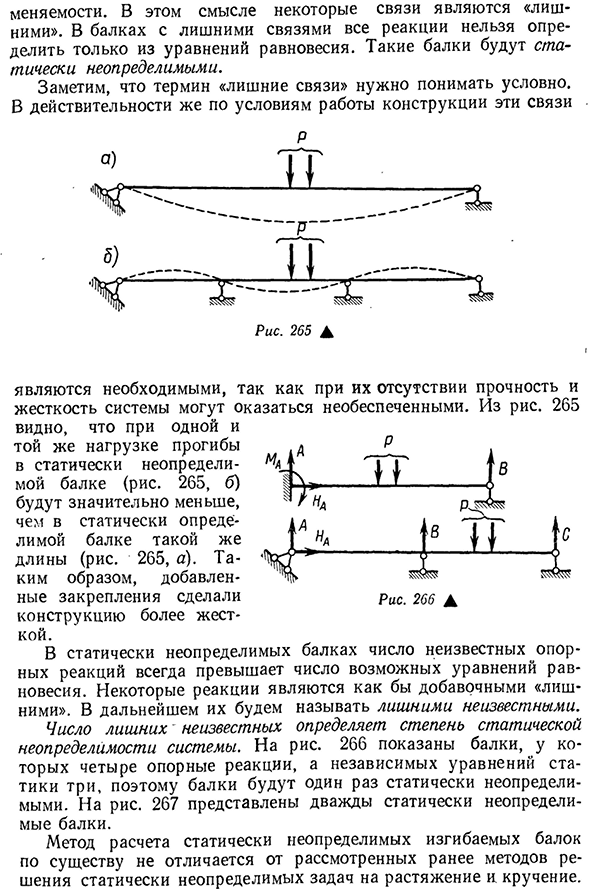
- Заметим, что термин «дополнительное соединение» следует понимать условно. По сути, в условиях строительства этих соединений П Рис 265Л Рис 266D При их отсутствии это необходимо, так как прочность и жесткость системы не могут быть гарантированы. Из рисунка. 265 при той же нагрузке наблюдается статическое неопределенное отклонение балки(рис. 265, Б) значительно меньше, чем статически определяемая балка той же
длины(рис. 265, а). Поэтому добавленные крепежные детали сделали конструкцию более жесткой. В статически неопределенных пучках число неизвестных опорных реакций всегда превышает число возможных уравнений равновесия. Некоторые реакции являются как бы дополнительными «экстра». В будущем мы будем называть их ненужными неизвестными. Количество
дополнительных неизвестных определяет степень статической неопределенности системы. Для риса. 266 показан пучок с четырьмя опорными Людмила Фирмаль
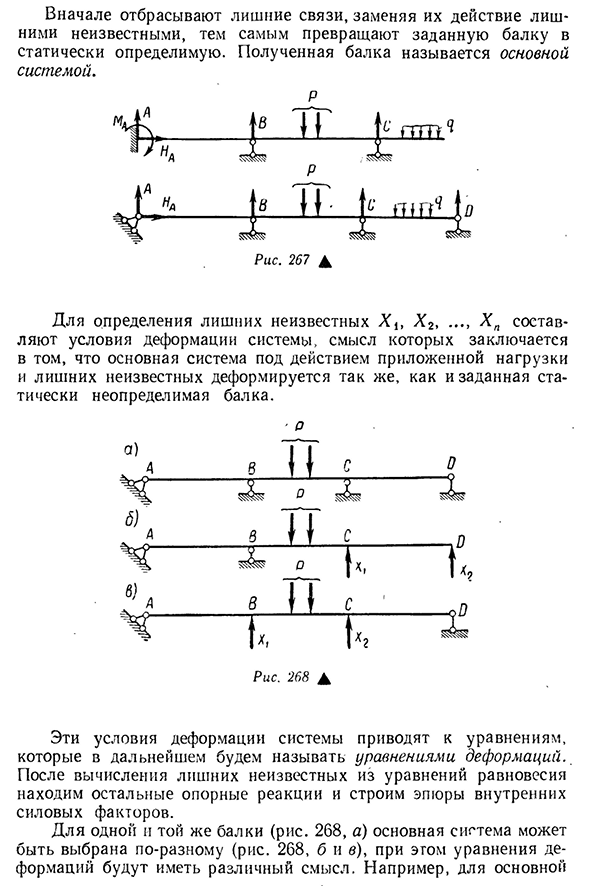
реакциями и тремя независимыми уравнениями статики, так что пучок становится статическим неопределенным в данный момент времени. Для риса. 267 представлена дважды статически неопределимых балок. Метод расчета статически неопределенной изгибной балки по существу совпадает с ранее рассмотренным методом решения статически неопределенной задачи растяжения и кручения. 305 во-первых, вы меняете предписанный луч на то, что может быть статически определено, отбрасывая ненужные связи и заменяя действие нежелательными неизвестными. Полученный
пучок называется основной системой. П П Рис 267А Для определения дополнительных неизвестных X2, xn — это условие деформации системы, смыслом которого является основная система под действием приложенной нагрузки и заданной статической нагрузки. — С. Рис 268А Условия деформации этих систем приводят в будущем к уравнению, называемому уравнением деформации. После вычисления избыточных неизвестных из уравнения равновесия найдите оставшиеся опорные реакции и постройте график
коэффициентов внутренней силы. Для той же балки(рис. 268, а) основная система может быть выбрана различными способами (фиг. 268, б и в) с уравнениями деформации будут иметь разные значения. Например, в основном случае 306г В И Рис 269а Дополнительные неизвестные Эта система показана на рисунке.Уравнение для модификации b, 268, имеет следующий вид США-0 и 0. Эти уравнения показывают, что полное отклонение точки C и точки y от действия неизвестной силы X}и X2 и полное отклонение от внешней нагрузки P находятся, по сути, в данной системе. Для некоторых задач при
выборе основной системы полезно отказаться от внутреннего соединения, а не от внешнего, например, обрезать балку и ввести шарнир (269). Максимальный изгибающий момент М. Смысл уравнения деформации в данном случае заключается в отрицании угла поворота поперечного сечения в уплотнении за счет действия силы P и неизвестного момента M: y b=B. Выбирая основную систему, во всех случаях необходимо убедиться, что она статически определима и геометрически неизменна.
Смотрите также:

