Оглавление:


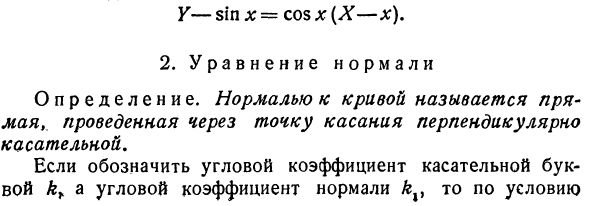


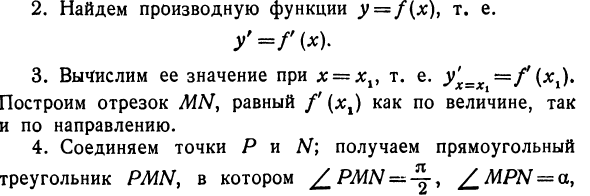


Простейшие применения производной
- Самое простое применение производных 1. Касательное уравнение Как показано в §3, геометрический смысл производной состоит в том, что ее значение равно угловому коэффициенту касательной в данной точке кривой, заданной уравнением y = f (x). Поэтому, если задана кривая y- / (x), на ней находится точка P с абсциссой xx, и записано уравнение касательной, они делают это. Сначала вычисляется ордината точки Ru.
Тем не менее, вы должны убедиться, что вы прикоснулись. Другими словами, выберите подходящий угловой коэффициент. Коэффициент угла касательной в этой точке равен k ^ f (xx), поскольку он равен производному значению. Поэтому уравнение касательной в точке кривой (xl9 f (xx)), заданное уравнением y ~ / (x), записывается в виде: V-PXX) = T (X ^ X-Xr). Пример 1. Напишите уравнение параболического тангенса у = х2-4х + 1 Вычислить ординату точки P в точке P с абсциссой xt = S. yx-Z2-4-3 + 1 = -2.
Пучок прямых линий, показано уравнение пучка С гл. II пишется как: Y-Y \ = k (X-Xx). Людмила Фирмаль
Найти производную. r = 2 * 3-4 = 2. Касательное уравнение параболы y-x2-4l: +1 в точке (3, -2) имеет вид y — (- 2) = 2 (x-3) Это становится. Пример 2. Напишите уравнение касательной для кривой y = sinx. Точка, где происходит касание, здесь не показана. Это должно быть понято следующим образом: Напишите уравнение, которое всегда может получить уравнение касательной для любой точки синусоиды. Возьмите точку (x, sin x), эта точка находится на синусоиде. Найдите производную: y ‘= cos.v. Во избежание путаницы координаты точек на касательной обозначены заглавными буквами X и Y.
Затем уравнение касательной синусоидальной волны в любой точке записывается в виде:Y — sin x = cos x (X — l :). 2. Нормальное уравнение Определение Нормаль кривой — это линия, которая проходит через точку касания, перпендикулярную касательной. Когда градиент выражается градиентом касательного символа kb и нормального kv,Вертикальность (Глава 11) kx = -y. Следовательно, нормальное уравнение
- Пример 3. Напишите нормальное уравнение для кривой, заданной уравнением y = x2-2 * 4-3 на этой кривой с абсциссой, равной 3. Поскольку точка находится на кривой, подстановка x = 3 в формулу y = x2-2a: + 3 дает свою ординату ^ = 6. 4. Подставим полученные данные в уравнение Обычно мы получаем Y — 6 = —3). 3. Угол между двумя кривыми Угол между двумя кривыми в определенном пересечении является углом между касательными Эти кривые нарисованы на перекрестках.
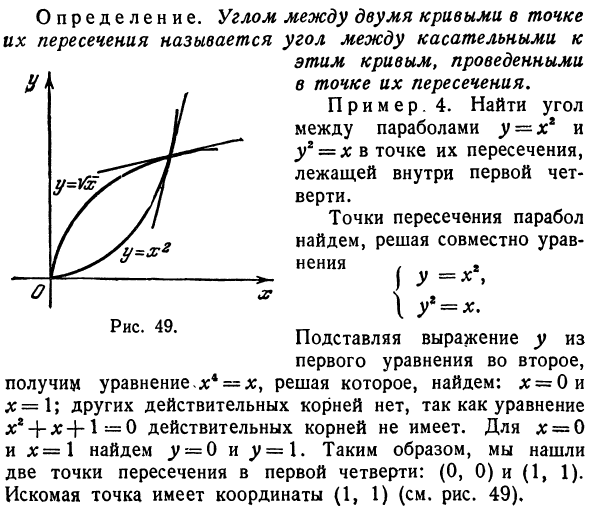
Пример. 4. Найти угол между параболой y ~ xl и y2 = x на пересечении в первой четверти. Найдите пересечение параболы и решите уравнение вместе. г \ Y = *> \ Подстановка уравнения y из первого уравнения во второе приводит к уравнению * 4 = x, и, решая это, уравнение x2-b: -b 1-0 не имеет реального корня, поэтому другое Настоящего рута нет. Если * = 0 и x = 1, вы найдете y ~ 0 и y = 1. Таким образом, в первом квартале мы нашли два пересечения, (0, 0) и (1, 1). Точка интереса имеет координаты (1, 1) (см. Рис. 49). Рисунок 49.
Найти функцию y = xr и производную функции y = yh (не используйте знак минус, потому что принимается во внимание Q1): y ‘= 2x, Y = — ^ (см. стр. 95). Угол между прямыми (касательными) определяется по уравнению К (1). II. Подставляя в него значения kx и kg, , T ~~ 2, 3 tgY = -j-> то есть tgY = -m. Следовательно, угол между параболой в точке (1, 1) Равно Y = arctan ^ — ^ j (найден тупой угол). Если кривая задается уравнением yf (x), а точка P получается с координатами (*!> / (^ J), тангенс этой кривой в точке P можно построить следующим образом (рисунок 50): , 1. Из точки P нарисуйте прямую линию, параллельную оси OXu, и отложите на нее отрезок PM. Рисунок 50г Направлено увеличение абсциссы с длиной, равной 1.
Если мы вычислим значение этих производных с je = 1, то = ^ = = 4- Это коэффициенты касательного угла. Людмила Фирмаль
Найти производную функции y = f (x). Это значит 3. Вычислите значение с x = xv, то есть y’x = x = f (xl). Создает сегмент MN, равный f ‘(n ^) как по величине, так и по направлению. 4. Соедините точки P и N. Получить прямоугольник Я ^ Треугольник PMNy с MPN = a PM = 1, MN = f (xj. Из этого треугольника, Поэтому мы заключаем, что JL / — искомая касательная. Фактически, эта линия проходит через точку P и имеет угловой коэффициент, равный f (xx).
Смотрите также:
| Производная | Вторая производная. Производные высших порядков |
| Правила вычисления производных | Возрастание и убывание функции |

