Оглавление:


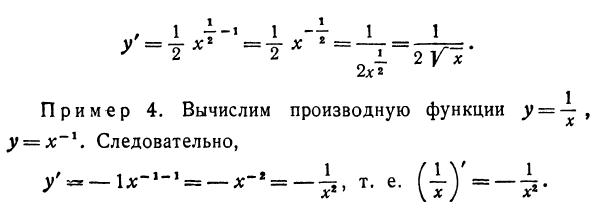



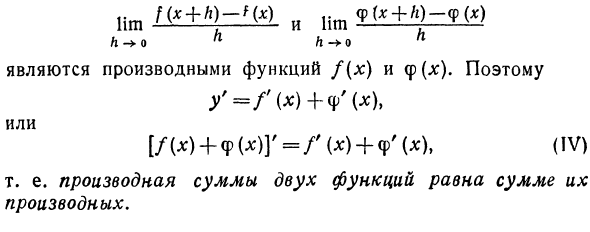

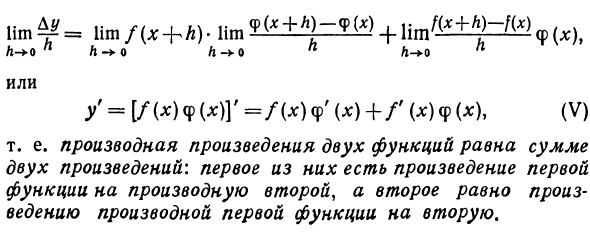

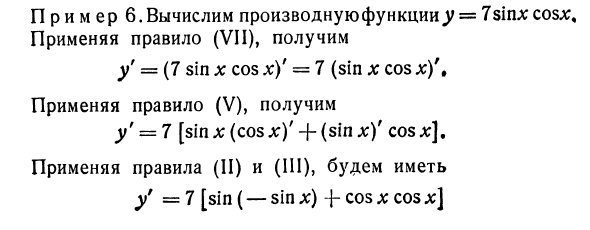

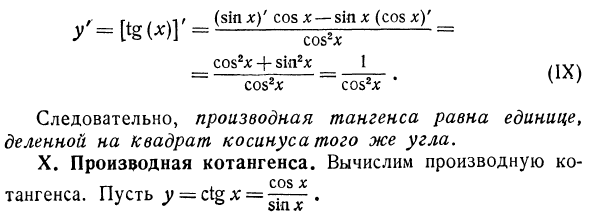

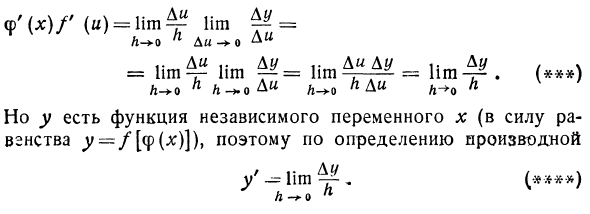

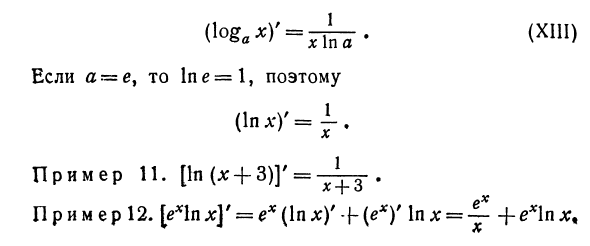

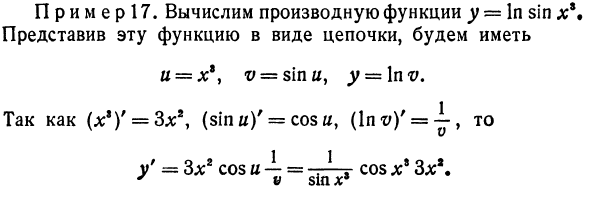


Правила вычисления производных
- Дифференциальные правила расчета В этом разделе производная рассчитывается для конкретного значения независимой переменной. То есть x считается константой, и его приращение h, а следовательно, и y, изменяется. Расчет производится по схеме, приведенной в §3. I. Производная степень.
Возьмите силовую функцию Y-X. «(1) Если вы дадите инкремент независимой переменной A, функция получит инкремент Du. y + by = (x + h) n; (2) Найти приращение функции Au> и вычесть член уравнения (1) из уравнения (2). Ay = (x + h) n — xn. (3) Расширяя (lg-fh) n согласно биномиальному уравнению Ньютона, правая часть уравнения (3) Dn = xn + nxn — 1 h + n («~ l) xn-zh * + … \ hn — xn
VI. Если функция сохраняет одно и то же значение a для всех значений независимой переменной, график представляет собой прямую линию, параллельную оси Ox, и уравнение имеет вид y = a. Конечно, поскольку касательная этой линии совпадает с самой собой, наклон касательной равен нулю, поэтому тангенс угла наклона также равен нулю, что означает, что производная равна нулю. Следовательно, производная константы равна нулю. ‘= 0. (VI) VII.
Производная функции, которая имеет то же значение, то есть производная от константы. Людмила Фирмаль
Предположим, что произведение результирующей функции f (x) задается константой a, т. Е. Y = a / (x). Найти производную от этого продукта. Используя уравнение (V) в этом разделе, Y = af (x) + a’Dx), Однако, поскольку постоянная производная равна нулю, a ‘= 0 и y’ = af (x), или [af (x)] ‘= of (x). (VII) Они говорят, что постоянные факторы могут быть взяты из производной. Примеры применения правила (b) — (VII) приведены ниже.
Пример 5. Рассчитать производную функции y = 2×9 + 5x *. Y ~ (2×9 + bxr) ‘записывается непрерывно. Применение правила (IV) дает y ‘= (2×9)’ + с использованием правила (VII) дает y ‘= 2 (l; 3)’ +5 (x2) ‘. Наконец, примените правило (1), чтобы получить окончательный результат y ‘= 2 • 3.v2 + 5. 2x = 6xr + 1 O *.
Пример 6. Вычислить производную функции >> = 7 sin * cos *. Применить и получить правило (VII) y = (7 sin a: cos = 7 (sin x cos x) \ Применить и получить правило (V) y ‘= 7 [sin x (cos x)’ + (sin x) ‘cosjc]. Применение правил (I) и (111) дает Y = 7 [sin (-sin x) -f cos x cos l:].
- Или упростить и y ‘= ■ 7 [cos2x-sin2x] = 7 cos 2x. х ^ «Я- грех х П р и м е р 7. Рассчитать производную функции y = -g—. Е. / = [* ± * L *] ‘. Применение (VII) дает y ‘= • y ^ l: 2 + sin l: ^; Применение (IV) приводит к y ‘[(xr)’ + (sin *) ‘]; Применяя (1), y ‘= [2x -} — (sin d :)’]; Применяя (II), y ‘= y [2l; + cosx]. Viii. Дифференцирование отношения двух функций. Для двух функций с известными производными их производные вычисляются по следующим правилам:
Прямая производная отношения двух функций равна дроби, где числитель — это разность между произведением производной числителя и знаменателя и произведением производной числителя и знаменателя, а квадрат знаменателя находится в знаменателе. гг / () Позвольте = тогда // () V = T (x) Φ (x) -Ix) d / (X) VI WW / f *)] 2 IX. Производная касательная. Пусть у ~ тгх. Для того, чтобы выразить грех х г- Получите касательную линию через синус и косинус, y = -. применимый Cos x Правило (VIII), затем (II) и (III),
F_G. _ (Sin *) ‘cos * -sin * (cos *)’ Y IS W] cos2 * _ cos2 * + sin2 * _ 1 cos2 * cos2 * (1) В результате производная тангенса равна единице, деленной на квадрат косинуса того же угла. Производная X. Котангенс. Вычисляет производную потому что * Tangent. Допустим, y = ctg jt =.Примените правило (VIII), чтобы получить: , __ (cos *) ‘sin x-cos x (sin x)’ Y sin2 * Применение правил (II) и (III) ,. h, -sin2 * -cos2 * 1 / vr. -iffi * — = — LAS- )]>, выразим ее в виде цепочки функций (гл. V, см. § 3). и = <р (х) () и у = ф (и). () — Уравнения (*) и () рассматриваются независимо друг от друга. Первый из них также дан как функция х.
Его производная равна cp ‘(x). Вторая определяет y как функцию независимой переменной. На практике, однако, невозможно рассмотреть эти два уравнения по отдельности. Они взаимосвязаны. Фактически, если вы даете x приращение A, u} как функция xy получает приращение A, но в то же время функция y имеет независимую переменную. Поэтому, если вы измените на Di, приращение Du будет меняться.
Его производная равна / ‘(u). Людмила Фирмаль
По определению производных o> ‘s = хм ^ Φ [X) n- + oh> / «= Рим Умножает последние два уравнения. При h 0 приращение Dm стремится к нулю, поэтому «P ‘() /’ («) = Hmf lim M = = lim ^ lim ^ = lim e Гм. () L-0 h h- »o A» H — + — Q h & U h- + 0 k Ho j / является функцией независимой переменной l. (Разница. Y = / [φ ()]), следовательно, по определению производной / ^ limЩ- 、 (*) Lol
Объединение уравнений () и () / = / ‘(A) ), (XI) То есть производная комплексной функции равна произведению производных цепочки функций. Пример 8. Вычислить производную функции y-sin4 x. Представьте y в виде цепочки функций: u = sinx и y = u \ (sin x) ‘= cos x и (u *)’ = 4m \, поэтому производная .y ‘есть произведение cos x-4a8 или y ‘= 4 sin8 l: cos l:. Пример 9. Рассчитаем производную y- \ gSx. Представим комплексную функцию y = ig3x в виде цепочки: u = 3x, у тгу. Вычислить производную: и ‘= 3, (tg and)’ = Q *; их Продукт дает желаемую производную / = s 1 3 cos2 и cos2Зх ‘ XII. Экспоненциальная производная.
Производная экспоненциальной функции определяется по правилу, выраженному следующей формулой. (Ах) ‘-a * a. (ХII) В частности, если a = e, ln = 1 и (E *) ‘= • — пример Эта формула имеет много применений. Пример 10. Найти производную (2ex + a *) ‘= (2ex)’ + — (ax) ‘= 2ex + ax \ pa. Xiii. Логарифмическая производная. Производная логарифмической функции определяется по правилам, выраженным формулой (Хп) Если a = e, lne = l, то (С l-) ‘= 1. Пример I. [(In (^ -1-3)] ‘= ^^ -. Пример 12. \ ex \ nx] ‘= ex (\ nx)’ \ — (ex) ‘1pln = — + ex \ nx.
Xiv. Производные обратных тригонометрических функций arctgjc и arcsin jc. Эти производные определены следующим образом: (Mctg *) ‘= JLgr (XIV) VT = и (Арксин xY = r-. (XV) X2 Пример 13. [arctgAr + arcsin = +. Пример 14. Найти производную функции y = Представим функцию .y в виде цепочки: u-x ‘+1, y ~ eu. (X3 +1) ‘= 3jc2, (eu)’ = eau to ‘= 3x * e «= 3x * e ** + K Пример 15. Найти производную функции y = * = arctglnAr. В формате: л -Arctgtf. (1pl 🙂 ‘= ~, (arctg and)’ = «тогда _J__ J_ 1 ^ «» * ‘1+ «2 ~ *’ 1 In * x •
Пример 16. Найти [arcsin (1 — x *)] ‘. Эквивалентная цепочка состоит из u = 1 — l; 2, y = arcsin и с того времени [1 — **] ‘= -2x, (arcsin uY = y ===, затем [arcsin (1 — **)]’ = Около 1 2x = -2л: / 1 —a2 V 1— (I- * 2) 2 ‘ По мере развития навыков вычисления деривативов вы можете делать презентации в виде цепочек. Это показано в качестве примера. Конечно, первый пример будет объяснен подробно. Поэтому, на первый взгляд, заметного упрощения нет.
Пример 17. Рассчитать производную функции y = In sin x *. Выражая эту функцию в виде цепочки, u = xr> v = sin u, y = \ nv. (Xr) ‘= 3×2, (sinn)’ = cosi, (ln /) ‘= j, тогда y’ = 3×2 cos и — = — pC-cos x8 Zl ^ Я грязный G8 Или после привлечения такого члена, Дy = nxn-lh + П (1Я-1) л: * 1 «1А» + .. • + А «. Разделим обе части последнего равенства на A, тогда n 1 • I Если A стремится к нулю, предел достигнут. limA * = 0, поэтому lim = nxn ~ 1, т.е. L o o l (* «) ‘= L *» — \ (I) То есть производная порядка равна произведению показателя степени и показателя степени с тем же самым основанием и показателем степени, уменьшенным на 1.
Пример 1. Рассчитать производную функции y = l: 1. Применяя правило оценки, y ‘= 5×9 ~ \ (т.е. D: 5)’ — 5l; Пример 2. Используйте производное правило для вычисления производной функции y ~ x или y = xL . / = Bx, -, = x ° = 1. Об этом следует помнить в следующей редакции. Производная независимой переменной равна 1. Примечание. При получении производного порядка мы рассматривали n как положительное целое число, но выражение остается верным, даже если это условие отклонено. Пример 3. Вычислить производную функции y-Y ^ x. Jl я у = х2. Где п -> —
Следующая формулировка дает первый множитель справа от последнего уравнения. Логарифмическая производная равна 1, деленному на логарифмический источник. В этом примере в sin x * y дается производная Логарифмические операции рассматриваются. оставшийся функция sinx *. Второй фактор читается следующим образом: Производная синуса равна косинусу, из которого был получен синус. Следовательно, производная cosjc8. Взятие подписи считается. Осталось х3. Производная этого уравнения равна 3×2, что является третьим фактором.
Пример 18. Поиск (arctg8 *) ‘. Здесь последняя (вторая) операция повышается до третьего уровня. Первая операция — получение арктангенса. Итак, сначала найдите производную порядка, получите 3 arctan2 x, затем получите производную Получите арктангенс, * 2. Умножьте то, что было получено 1-е-х У нас есть y ‘= 3 arctg2 * • —ij-. Пример 19. Поиск (arctg.v8) ‘. Где последняя (вторая) операция — захват арктангенса, а ее производная 1 l ^ 5) 2 • Поскольку первая операция — это куб, Производная 3×2. Умножение полученного выражения дает (Arctg x’y = •
2х2 Пример 4. Рассчитать производную функции y x. Таким образом, 1 _ _ f IV II. Производная синуса. Дай мне = грех л: (1) Если вы даете x приращение A, y изменяется и становится равным y + Ay = грех (n; 4-A). (2) Найдите приращение A y и вычтите член для каждого члена из уравнения (2) и уравнения (1). Dy = sin (x -f L) — sin x или после преобразования, A >> = 2sinyCos (x + A). (3) Разделите обе части (3) уравнения на приращение независимой переменной. 2sinAC0S (, + j) sin- | t = -r- <4> 2 A —Предел достигается при условии (►). получить преступление Обод lim cos fx • (5) h th n h- + o C h-> o \ 1J 2 Если аргумент стремится к нулю, отношение синуса к аргументу равно 1 (см. Главу VI, §2),
Кроме того, косинус является непрерывной функцией (см. VI, § 5), поэтому lim cos (x) = cos *. Учитывая вышеизложенное Аю \ 1 / Получить lim ^ = cosjc из уравнения (5). Это значит Л о П (Грех х) ‘= cos l:. (II), То есть производная синуса равна косинусу того же угла.III. Косинус производная. Производная косинуса может быть получена так же, как и метод получения производной синуса.
Только в этом случае следует применять формулу разности косинусов. После того, как вы выполнили все расчеты, вы увидите (Cos xy = -sin x, (III) Другими словами, косинус производная равна синусу того же угла, взятого с противоположным знаком. Внутривенно Производная суммы двух функций. Предположим, что производные функций f (x) и φ (q;) известны. Вам нужно найти производную от их суммы. Учитывайте сумму y = f (x) + φ (x). (1) Если x получает приращение hy, каждая функция получит приращение, а их сумма также получит приращение y + Ay = f (x + h) + 0. ton = «w / CH -«) — / M + Hsh F (‘+ ) — ), hоПh-> оПhоП Поскольку f (x + h) -f (x) является приращением функции f (: c), а φ (x +)) — φ (г) является приращением функции φ (x),
lim / («+ ) — ‘() и центральная школа» P («+») — ph («) h o fl h-> o L Производная функций f (x) и φ (л :). так / = / ‘() + Φ’ (), или [/ () + ΦMJ ‘= /’ () + φ ‘(*), (IV) То есть производная суммы двух функций равна сумме этих производных. V. Дифференцирование произведения двух функций. Предположим, вы знаете производные функций f (x) и
= / ()
Φ <> + / C +++) — / ()) Φ (x). (5) с того времени lim V (x + h) -V (x), {x) ч- оп ободок Ноги — ►O P Далее, когда предел уравнения (5) достигается при условии A — »- O,
A- * o ft o l A- ^ o A или / == [/ () φ ()] ‘= / () φ’ () + / ‘(X) φ (*), (V) То есть производная произведения двух функций равна сумме двух произведений: первая функция — произведение первой функции и второй производной, вторая — первая функция и вторая Продукт производной от.
Смотрите также:
| Касательная | Простейшие применения производной |
| Производная | Вторая производная. Производные высших порядков |

