Оглавление:



Понятие о центре изгиба
- Концепция гибочного центра Как упоминалось выше, напряжение сдвига в поперечном сечении тонкого стержня при изгибе (например, двутавровой балки или канала) определяется по следующей формуле Fu5°TS Для риса. Показаны 210 графиков касательных напряжений в поперечном сечении двутавровой балки. Можно также построить
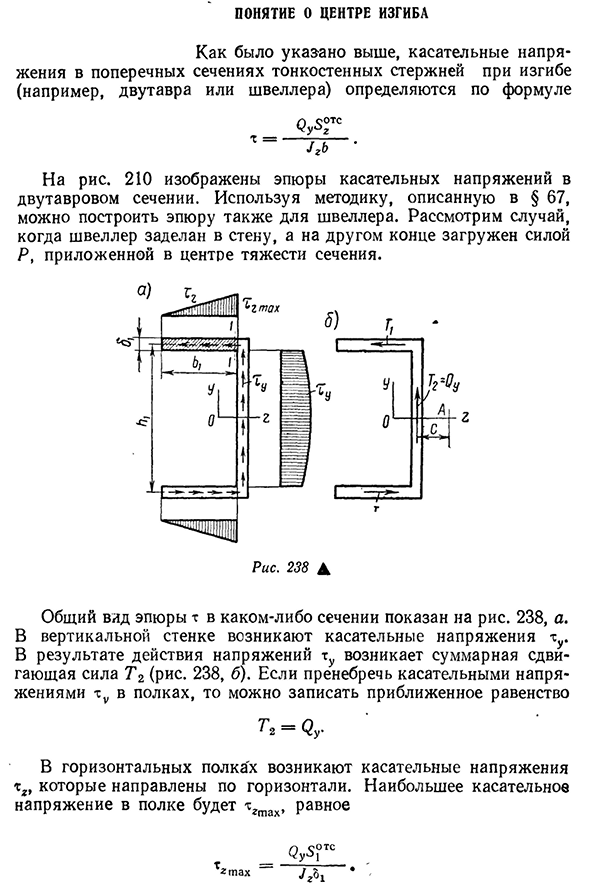
канал, используя методы, описанные в §67. Рассмотрим случай, когда канал встроен в стенку, а другой конец нагружен силой Р, приложенной к центру тяжести секции. Рис 238D Сумма графиков t любого sectionvld показана на рисунке. 238, а. Н
а вертикальной стенке возникает тангенциальное напряжение Tu. В результате действия Людмила Фирмаль
напряжения Tu возникает суммарная сила сдвига T2(рис. 238, б). Если пренебречь касательным напряжением ту на полке, то можно написать приближенное равенство ^2=^г^ Горизонтальные полки имеют касательное напряжение, которое направлено горизонтально. Наибольшее касательное напряжение стеллажа равна основным ■ г-осьминог 266 здесь 5?ТС-статический момент площади полки
относительно оси 0г \ И так оно и есть., gtah=-2/G01 колодки » 1* Общая сила сдвига стойки равна площади участка касательных напряжений, умноженной на толщину стойки, ^Т Х5^1 Два. 6? И.& Нижняя полка имеет точно такую же силу сдвига, как и верхняя полка,но она направлена в противоположном направлении. Две силы T1 образуют пару в один момент М, Т. Н.= Б2, Л? (8.39) Таким образом,
- из-за тангенциального напряжения существуют три внутренние тангенциальные силы, показанные на диаграммах Xu и Tg. 238, б. из этой цифры ясно, что сила?! И Т2 стремится повернуть поперечное сечение канала относительно центра тяжести в том же направлении. Таким образом, в поперечном сечении канала возникает внутренний крутящий момент в направлении против часовой стрелки. Поэтому
при изгибе швеллера балка силой, приложенной к центру тяжести сечения, перекручивается одновременно с балкой. К основному вектору и основному моменту можно привести три тангенциальные силы. Величина основного момента зависит от положения точки, в которой действует сила. Вы можете выбрать точку а, где главный момент равен нулю. Эта точка называется центром изгиба. Уравнять момент касательной силы до нуля: %ОП=м^-с^С ^ С=О,
получить Для выражения 267 (8.39), наконец, найдите расстояние от оси Людмила Фирмаль
вертикальной стенки до центра изгиба: ■После- Когда внешняя сила приложена к центру изгиба, а не к центроиду сечения, для того же центроида создается тот же момент, что и тангенциальная сила внутри, но с такой нагрузкой противоположного знака(рисунок). 239) канал не крутится, а только изгибается. Именно поэтому точка А называется центром изгиба. Подробное описание расчета тонкостенных стержней приведено в главе XIII
Смотрите также:
| Допускаемые напряжения | Определение перемещении в балках при изгибе общие замечания |
| Примеры расчетов при действии сосредоточенных сил | Устойчивость круговых колец и труб |

