Оглавление:

Касательная
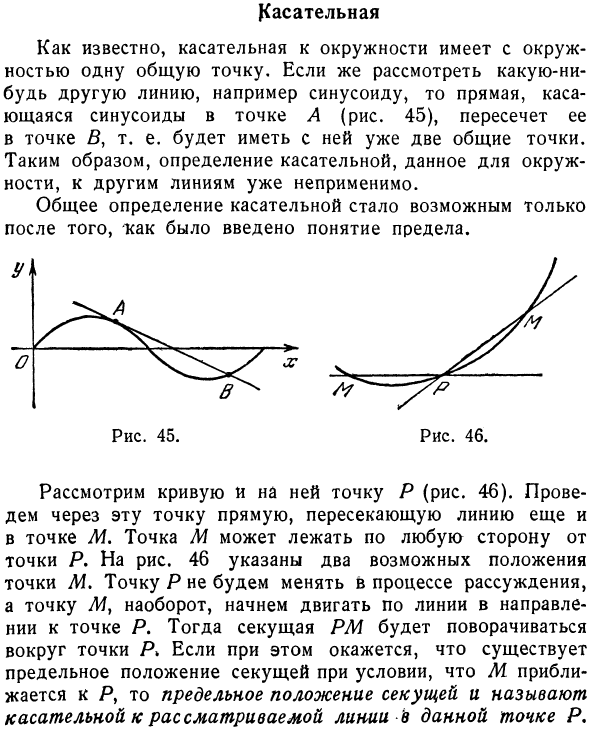
- Касательный Как известно, касательная к окружности имеет одну общую точку с окружностью. Принимая во внимание другие линии, такие как синусоида, линия, которая касается синусоиды в точке A (рисунок 45), пересекается в точке B.
- Поэтому определение касательной, данное кругу, не может быть применено к другим линиям. Общее определение тангенса было невозможно до тех пор, пока не было введено понятие пределов. в Рисунок 45.
Другими словами, уже есть две общие черты. Людмила Фирмаль
- Рисунок 46. Рассмотрим кривую и точку P над ней (рисунок 46). Нарисуйте линию через эту точку, которая также пересекает линию в точке М. Точка M может быть размещена по обе стороны от точки P.
Вместо изменения точки P в процессе выведения, наоборот, точка yI начинает двигаться вдоль линии в направлении точки P. Когда M приближается к P, предельное положение секущей называется касательной к проблемной линии в данной точке P.
После этого секущий РМ вращается вокруг точки Pb. Людмила Фирмаль
Смотрите также:
| Решение задач на нахождение пределов | Производная |
| Скорость | Правила вычисления производных |

