Предел lim (1+jc)*. Число e

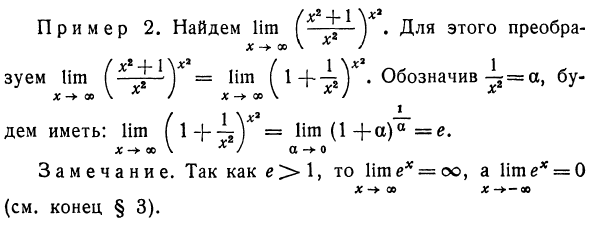
Предел lim (1+jc)*. Число e

• Limit lim (1 + jc) *. Номер е О Х 1 Рассмотрим функцию (1 + x) x. Если x стремится к нулю, содержимое скобок приближается к единице. Если x не равно нулю, скобка не равна 1. Кроме того, если x больше нуля, скобка больше 1, а если x меньше нуля, скобка меньше 1.

• 1 рассмотрим lim (1 • не понятно чем он равен О Х Это происходит потому, что если q:> 0, числа больше 1 увеличиваются в положительную степень, а если l: <0, числа меньше 1 увеличиваются в отрицательную степень.

Тем не менее, вы можете указать, что это ограничение существует. Людмила Фирмаль

Это доказано в подробном курсе. Число, равное этому пределу Письмо е. Поэтому число e называется lim (1 — {- *) *. О Х Число e является иррациональным числом, и его приближение (максимум 1/1000) 2.718.

• В математике это видно так же часто, как и число I. Оказалось очень удобным использовать е в качестве основы логарифма. Логарифм с основанием е называется натуральным логарифмом. Они указаны с помощью In. Эти логарифмы в основном используются для теоретических задач. п ^ 1

Пример 1. Поиск лим-значения- • =. *;, № 00 Получите это как n— »oo x -» — 0. так ободок(X2 4- \ x2 -. Для этого преобразования .. -х Дж Дисплей lim = lim ^ * = bu- Есть Dem: lim f 1 == Hm (1-f-a) a = х так V х) а-> о Замечания.

Так как е> 1, известь * = оо, известь * = 0 X 00 * -> — 00 (См. §3 конец). Людмила Фирмаль

Смотрите также:

Предмет высшая математика

Определения предела	Непрерывные функции
Свойства пределов	Решение задач на нахождение пределов