Оглавление:


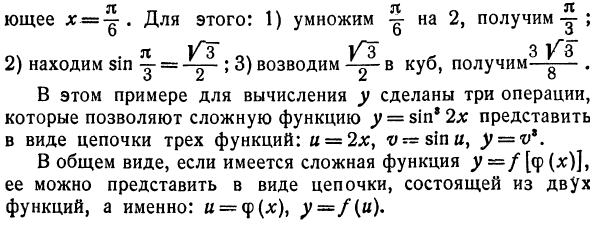

Функция от функции, или сложная функция
- По функции или сложной функции Часто при решении многих задач вам приходится иметь дело с «функциями функций». «Функциональные функции» также называют сложными функциями. Позвольте мне привести пример того, что это значит. Пример 1. Цель удаляется из оружия, которое стреляет из цели. Расстояние «оружие-цель» является функцией времени. Стрелок устанавливает угол прицеливания в зависимости от расстояния.
Следовательно, угол прицеливания является функцией расстояния «пистолет-цель». Однако расстояние «орудие-цель» уже является функцией времени, поэтому угол прицеливания является функцией времени. Следовательно, угол прицеливания является сложной функцией, то есть функцией функции. П р и м е р 2. Когда заданы функции u = xr и y = u + u1. Функция y может рассматриваться как функция независимой переменной x. Фактически подставим вместо выражения u = xi: y = x * + (x2) 2 = x2-L ^ где y — функция функции. Пример 3. В будущем очень важно уметь представлять сложные функции в виде простых функциональных цепочек.
Рассмотрим функцию φ = 1-µ2 и u = s’mt. φ является функцией функции, φ = 1 — sin21-cos 2t. Людмила Фирмаль
Давайте проиллюстрируем на примере, что это значит и как это делается. Пример 4. Рассчитать значение функции ^ logcosx, соответствующее значению x = 2l. Для этого: 1) Рассчитать значение cos2ji. $ 2π = 1; 2) Рассчитать лгл. 0. Чтобы вычислить -y = lgcosA, в этом примере нужно было выполнить два действия.
- Другими словами, потребовалось две операции. Эти две операции представляют сложную функцию y = logcosx в виде простой цепочки. u = cos x и y = \ g и. Последние два уравнения эквивалентны указанным. Пример 5. y = sin8 2x. Рассчитайте значение ^ и соответствующий
Для этого 1) ^ умножается на 2, чтобы получить у. Очень хорошо Л / З «ВЧ В *» 3 2) Найти грех у =; 3) Когда-> y- возводится в куб, -g- получается. В этом примере три операции выполняются для вычисления y, и комплексная функция y-sin * 2x может быть представлена как цепочка из трех функций. n = 2x> v — sin и y = v *. .Y = f [f (x)], то в виде цепочки из двух функций: u == (f (x) 1 y = f (n)) Может представлять
Вообще говоря, если существует комплексная функция. Людмила Фирмаль
Смотрите также:
| Примеры и определения | Приращение функции |
| Область существования функции | Исследование функции sin* при значениях |

