Оглавление:







Касательные напряжения при изгибе
- Напряжение сдвига при изгибе В отличие от чистого изгиба в поперечном сечении балки присутствует не только изгибающий момент, но и поперечная сила. Таким образом, в поперечном сечении наряду с нормальными напряжениями возникают и тангенциальные напряжения. Исходя из закона четности касательных напряжений, последнее также возникает на продольных сечениях, вызывая сдвиги отдельных волокон, связанных друг с другом. *Если главная ось не
является чисто изгибающей осью симметрии, то внутренний изгибающий момент представляет собой пару в плоскости, параллельной главной плоскости стержня、 / Это = расстояние а-здесь, 5 и. — Центробежный момент инерции и статический момент полусегмента относительно оси выхлопного газа. Эффект сдвига 228 нарушает гипотезу о плоском поперечном сечении
при поперечном изгибе, и плоское поперечное сечение перед деформацией слегка Людмила Фирмаль
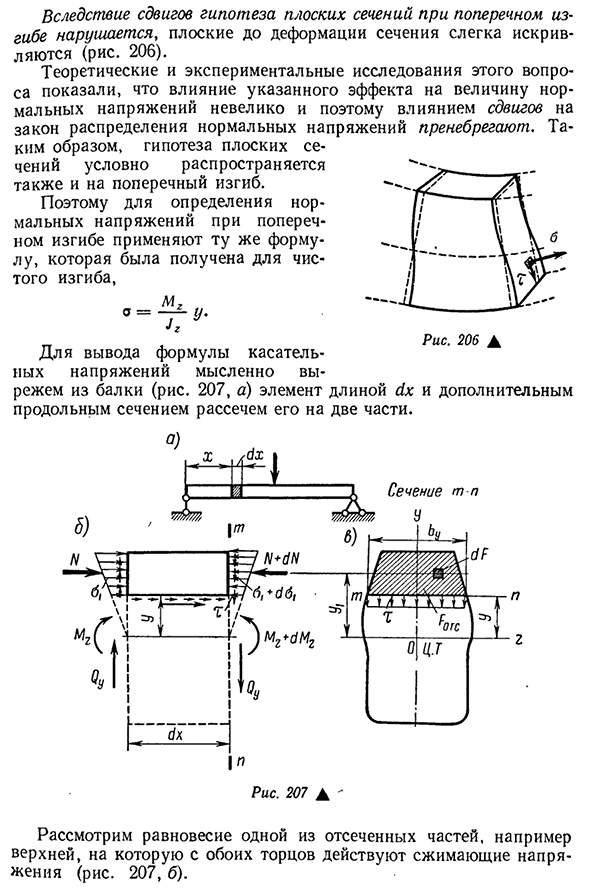
искривлено(рис. 206). Теоретические и экспериментальные исследования этой задачи показывают, что этот эффект мало влияет на величину нормального напряжения, поэтому гипотезы о плоском сечении, следовательно, о законе распределения нормального напряжения, также условно распространяются на поперечный изгиб. Поэтому та же формула, полученная для чистого изгиба, используется для определения нормального напряжения при поперечном изгибе,
М2 °=- — — — г. г Чтобы мысленно вывести уравнение касательного напряжения, нужно нарисовать балку (рис. 207, а) длина YX элементов и дополнительные продольные сечения разрезают его на две части. Рис 207Л — Рассмотрим равновесное состояние одной из несвязанных частей, например, верхней, которая является сжимающим напряжением с обоих концов. 207, б). 229C правая сторона каждой площадки a? Так как правый изгибающий момент
- больше левого изгибающего момента при значении AM2, то б / о! Сила сжатия, действующая на отрезную часть правой стороны, больше, чем на левую、 Тонны У1ар. (И> Р Р2• * 2Г ОТС ОТС ОТС Этот Интеграл распространяется на область отсечной части ГТС, заштрихованную на рисунке. 207, ст. Интеграл выражения (а) представляет собой статический момент отрезной части для нейтральной оси Og c=I y^p — ** отн И так оно и есть. 5°’°. • > т г г г Для того чтобы отрезная часть элемента DX находилась в равновесии, на продольном сечении должно быть приложено тангенциальное напряжение t(см. Рисунок). 207, б). Эти напряжения создают
тангенциальную силу YT,и в равновесии 2X=0 должна быть равна силе DM: at=ay, Или В=^8°g GS. (8.11) однако для определения напряжений t необходимо знать закон их распределения по ширине балки. Здесь тоже необходимо применить гипотезы для решения проблемы. На практике необходимо связать этот вопрос с секционной формой. В большинстве поперечных сечений напряжение T предполагается равномерно распределенным по ширине поперечного сечения. При таких допущениях сила сдвига dt определяется выражением
ДТ=tdhw, Здесь U-ширина поперечного сечения в точке, где определяется напряжение сдвига. Равенство 230º(8.11), мы Людмила Фирмаль
получаем amg5 ° ts Но ЛМ C1X1G БУ Наконец, у нас есть . Эта формула называется формулой Журавского,который впервые установил наличие касательных напряжений в изгибе. Исходя из закона четности касательных напряжений, полученная формула также определяет касательные напряжения в поперечном сечении стержня точки, расположенной на линии t-p(см. рисунок). 207). Из Формулы (8.12) видно, что тангенциальное напряжение изменяет высоту сечения по тому же закону, что и величина -. В прямоугольное сечение, г=г = сопз!, Закон распределения тангенциального напряжения по высоте сечения будет таким же, как и значение
статического момента отсечки детали 5°TC*. Поэтому касательное напряжение в этих точках также равно нулю. Рассмотрим распределение касательных напряжений в нескольких типах поперечных сечений. P R I m o u g o l l n o s e h e n I e. возьмите любую точку K на расстоянии от нейтральной оси y (рис. 208). Проведем поперечное сечение параллельно оси этой точки Og\ширина этого сечения будет равна U=B. В результате (см.§48), История ※Обратите внимание, что отрезная часть может быть взята как верхняя (заштрихованная), так и нижняя. Для обеих частей 5°TC является одинаковым по абсолютной величине. Это вытекает из условия, что
статический момент всего сечения равен нулю для нейтральной оси. Известно 231как, Заменить на Значение, полученное в выражении (8.12), равно — > Б Рис 208А 2-1.- 1’1′ Тсс. — Позже. К Ноль. Один. Около Формула (8.13) показывает, что напряжение сдвига по высоте поперечного сечения изменяется по закону параболы квадрата. С Y=±2, t=0 и с y-0 з ОУ з ОУ ttah= = Т ‘ ~Р~’ Для риса. 208 приведен общий вид участка т, в его конструкции вертикальная ось численно равна касательному напряжению, нанесенному перпендикулярно прямой, параллельной оси ОП. Особенностью данного сечения является резкое изменение ширины сечения при перемещении от стенки двутавра к
его полкам. В основном боковая сила воспринимается стенками, а доля полок составляет небольшое количество. Рассмотрим любую точку K(рис. 209). Проведем через эту точку линию, параллельную оси ox. Статический момент верхнего среза (заштрихован на рисунке. 209) можно найти как сумму двух квадратов и статического момента P2: 5G=P1U1+P2U2- Это выражение справедливо, если точка K находится в пределах вертикальной стены, то есть пока значение y находится в пределах диапазона Диаграмма касательных напряжений вертикальной стенки показана на рисунке. 209. Для определения тангенциальных напряжений в полке двутавровой балки 232в следует отметить, что в каждой точке имеются тангенциальные напряжения фигур Tu и T2. 209). Когда вы применяете формулу (8.12) и определяете Tu, ширина сечения резко меняется, поэтому график t скачет, и появляется пунктирная линия, как показано на чертеже.
Однако для определения Ту нельзя использовать формулу (8.12). Таким образом, проблема величины и закона распределения касательных напряжений в горизонтальной области полок остается нерешенной. Однако из-за того, что в этих сечениях тангенциальные напряжения ту малы и практически не влияют на интенсивность пучка, они обычно неинтересны и поэтому не влияют на прочность пучка. Тангенциальное напряжение TG гораздо интереснее. Предполагая, что они равномерно распределены по толщине полок, можно также определить их по общей формуле (8.12), но лучше использовать статический метод отсечения детали. <gots_R „ Здесь Gots и g/1 взяты, как показано на рисунке. На этом рисунке также показан вид графика касательных напряжений как в I-м сечении
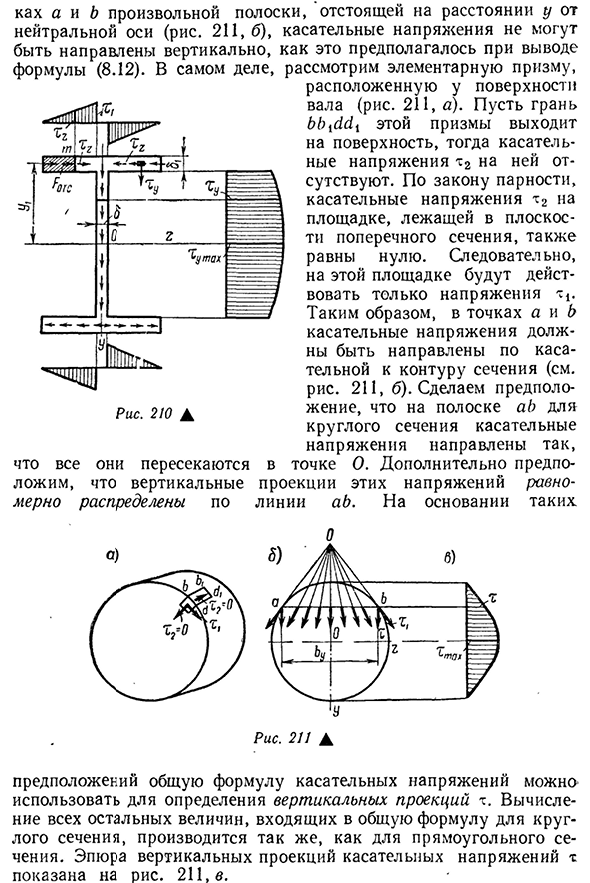
вертикальной стенки, так и в горизонтальной полке. Направление этих напряжений также указывается. К Л Ю ч е в ы е С Л О В а задача определения касательного напряжения сложна в той части, которая очерчена кривой. Поэтому, например、- 233 А и в любой полосы, расположенной на расстоянии y от нейтральной оси(рис. 211, б), касательное напряжение не может быть направлено перпендикулярно, как это предполагается при выводе формулы (8.12). На практике рассмотрим основную призму вблизи поверхности вала(рис. 211, а). Пусть b^c1c1 X этой призмы выходит на поверхность, на ней нет касательного напряжения T2. По закону четности касательное напряжение T2 на участке, находящемся в плоскости
поперечного сечения, также равно нулю. Поэтому в точках a и d тангенциальное напряжение должно быть направлено по касательной к контуру узла(см. рис. 211, б). Предположим, что на ад-полосе круглого сечения касательное напряжение направлено в точку O.In кроме того, эти напряжения рекламной линии бросают Все они пересекаются во лжи, а вертикальные равны-то есть они размерно распределены на основе таковых. Отчет Но) 5) / Вт б) Рис 211А Общая формула тангенциального напряжения может быть использована для определения » вертикальной проекции T. график вертикальной проекции тангенциального напряжения t показан на рисунке. 211, ст. Все, что говорится о круговом сечении 234, относится к нескольким другим типам поперечного сечения. Например, даже в треугольном сечении необходимо определить проекцию касательного напряжения на вертикальную ось.
Смотрите также:

