Оглавление:





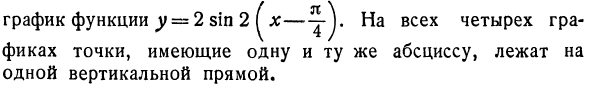

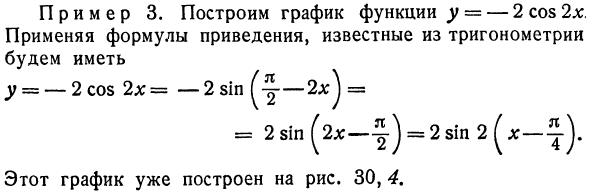

Тригонометрические функции. Радианная мера угла
- Тригонометрическая функция. Угловое радианное измерение Напомним измерения угловых радианов, прежде чем рассматривать тригонометрические функции. В радианах мера центрального угла представляет собой отношение длины дуги к радиусу дуги. Если R — длина радиуса, а / — длина дуги, радиан мера дуги x выражается как Я / G (1) х = Поскольку / и R измеряются в линейных единицах, из (1) видно, что x является абстрактным числом.
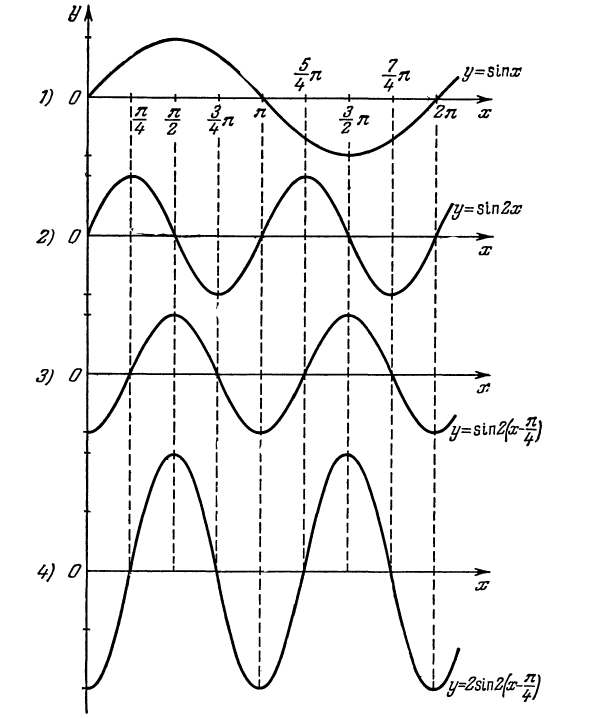
Из формы это известно 180 (2) 2nRa ° nRa / = 360 < /. Следовательно, радиальная единица измерения угла a ° равна _J__pa R 180 ‘ Найти из уравнения (2) и получить уравнение для измерения степени угла с точки зрения радиан. 180 ° х (3) а ° = L График функции y = 2 sin 2 y x — ^ — j. На всех четырех графиках точки с одинаковой абсциссой находятся на одной вертикальной линии.
Где a — это мера степени центрального угла на основе дуги Людмила Фирмаль
График функции y = 2 sin 2 y x — ^ — j. На всех четырех графиках точки с одинаковыми абсциссами находятся на одной вертикальной линии.Рисунок 30 Вы можете построить косинус, используя указанный метод построения синусоидальной волны. Вот пример.Пример 3. Построить функцию y = -2 cos 2x. Применить известную формулу сокращения из тригонометрии y = -2 cos 2l: = –2 sin- = Этот график уже показан на рисунке. 30, 4.
Пример 1. Найти радиан измерения под углом 30 °. Подставляя в уравнение (2) вместо числа 30, я «30 я 180-6 ‘ Пример 2. Найти шкалу угловых порядков с радианами 0,8. Подставляя в уравнение (3) l: = 0,8, o_ 180 ° -0,8 ~ Я Или, грубо говоря, я предполагаю, что «3.14 ° найдено» 45 ° 50 ‘. L Поскольку u является константой, уравнение (2) устанавливает прямую пропорциональность между числами x и a. Триангуляция вводит отрицательные углы в дополнение к положительным углам, поэтому радианы углов могут быть отрицательными. Например, радиальный угол –90 ° Мера Граф функций y = s \ nx При построении тригонометрических функций это можно сделать без таблицы. Для этого сделайте это (рисунок 26):
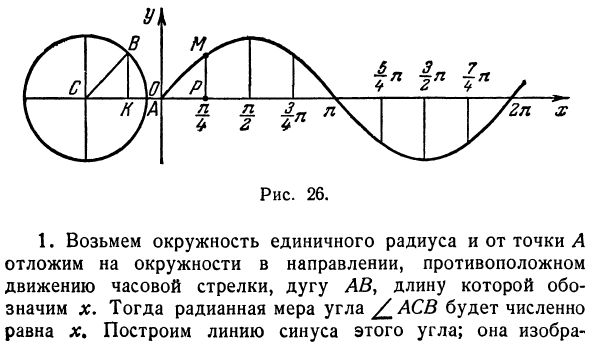
- VI o v \ o m / 0 \ / l | l 1ya. \ №2 4 / A L. 1 „l \» r H U2n «x Рисунок 26 1. Возьмите круг с единичным радиусом и поместите круг AB в сторону от точки A в направлении, противоположном движению по часовой стрелке. Длина дуги AB обозначена х. Измерение угловых радиусов ASB численно равно x. Нарисуйте линию синуса под этим углом. Она сфотографировала ВЧ сегмент. Поскольку R = 1, знак угла был найден К б Как отношение, оно численно равно длине короткого участка. 2. Получите оси координат (Рисунок 26).
На оси Ox отложите отрезок OA, длина которого равна длине x дуги AB. Сегмент PM, перпендикулярный оси, равен длине сегмента KV. Тогда JaU = / C5 = sinx. Следовательно, координаты точки M равны x и sin jc. Когда вы завершите эту конфигурацию для различных дуг, вы получите набор точек на графике функции Функция sin является периодической, а период является вторым. Это уравнение для любого значения х грех (d; + 2d) = грех l;. Граф функций <y = sincoAr Если вы измените аргумент с 0 на второй, синус принимает все значения от -1 до +1. Увеличение аргумента еще раз повторяет значение синуса из-за периодичности.
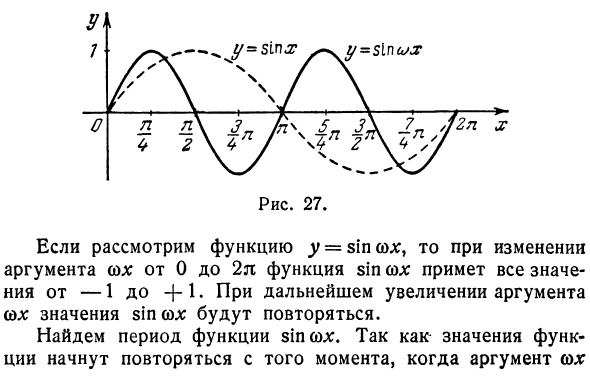
Учитывая функцию y = sin sox, меняя аргумент sod: с 0 на второй, функция sin ss принимает все значения от -1 до +1. sol: Если значение аргумента увеличивается, значение сои повторяется. Найти период функции sin sx. Поскольку значение функции начинает повторяться с момента аргумента Отсюда получаем х = ~.
При равенстве 2π период задается уравнением cox = 2π. Людмила Фирмаль
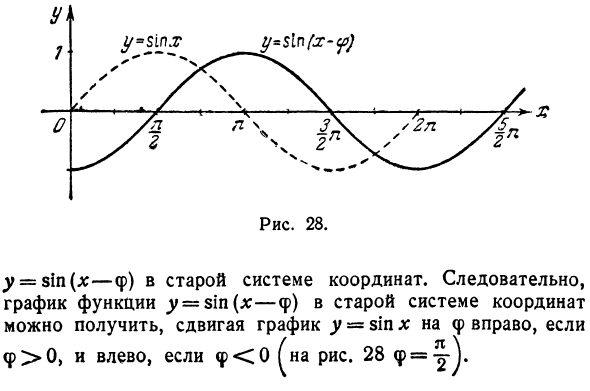
Следовательно, существует период действия греха и греха. на самом деле sin co ^ x + ^ j = sin (кокс + 2π) = грех кокс. Поэтому функция y = sinx имеет график, показанный на рисунке. 27. Если ω> 1, график y = sin ss сжимается по сравнению с графиком <y = sinx. Если 0 <ω <1, график растягивается (на рисунке 27 ω = 2). График функции ^ = грех (х— <р) Пройдите от старых осей к новым осям. Началом осей является точка (<p, 0). Старые координаты представлены новыми координатами следующим образом (см. § 2 главы 3): х = х + ср, у = у. Подстановка этих уравнений в уравнение jr = sin (x — φ) дает y = sinx. Другими словами, график функции ^ = sinx в новой системе координат выглядит так же, как график функции.
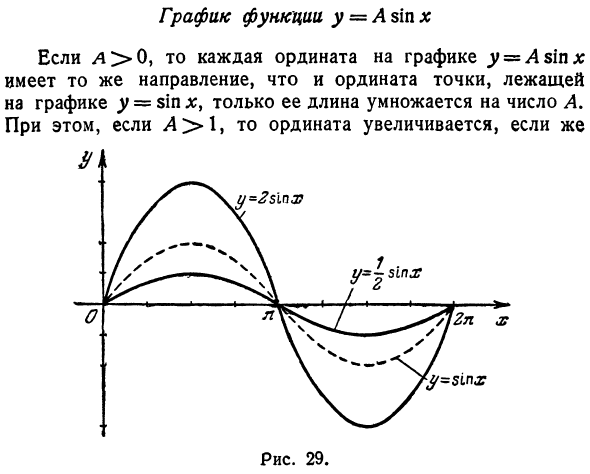
Рисунок 28. ^ y = sin (x: -ph) в старой системе координат. Следовательно, сдвигая график y-sin x вправо на φ, можно получить график старой функции системы координат 0 и Φ <0 (Φ = ˜ на фиг. 28).График функции y = A sin x Если Λ> 0, каждая ордината на графе y = Asipx имеет то же направление, что и ордината точки на графе y = sin x, и только ее длина умножается на числовое значение A. Рисунок 29
После этого L <1 уменьшается. Если L <0, ордината меняет направление на противоположное. Рисунок 29 показан График функций y = 2 sin x и y = -k-sin x. Следовательно, уравнение = sin sinω (x — cp) определяет кривую на плоскости, называемой синусоидой. Фактор ω, называемый частотой, влияет на распространение синусоиды в направлении оси Ox. Кроме того, если 0 <ω <1, синусоида растягивается, но если ω> 1, она сжимается.
Коэффициент φ называется фазой. Значение в целом влияет на смещение синусоиды вдоль оси Ox. Если φ положительное, сдвиг вправо, а если φ отрицательный, то сдвиг влево. Коэффициент A называется амплитудой, и его значение влияет на распространение синусоидальной волны в направлении оси Oy. Рисунок 30 показывает последовательную структуру Еще ниже — график График функции y = sin lg, ниже график функции y = sin 2lg, Выше фото Функциональная графика И внизу
Смотрите также:
| Параллельный перенос осей координат | Показательная функция |
| Исследование функции у = ах1 + Ьх + с | Логарифмическая функция |

