Оглавление:


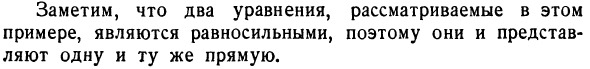

Система двух уравнений первой степени
- Система двух уравнений первого порядка Две линии на плоскости могут пересекаться, быть параллельными (то есть не пересекающимися) или объединяться (в этом случае можно сказать, что они пересекаются в каждой точке).
Рассмотрим систему из двух уравнений Axx + Bx + Cx = 0, Rxx + Br2 + C2 = 0 Решение системы означает поиск значений x и y, которые удовлетворяют как первому, так и второму выражению.
Каждое из этих уравнений является линейным уравнением. Людмила Фирмаль
Однако, поскольку x и y определяют точки для решения системы, это означает нахождение точек как в первой, так и во второй линиях, то есть нахождение пересечения линий.
Пример 1. Найти пересечение двух прямых. 2x — \ — 3y-8 = 0, 4x-y-2 = 0 Решение этой системы дает x = 1, y = 2. То есть линии пересекаются в точке (1, 2) (рисунок 17). Пример 2. Найти пересечение двух прямых. 4x + 2y = S, 2x + y = 5. Решение этой системы дает: у = 5-2 *, 4х + 2 (5-2л 🙂 = 8, 4л: + 10-4 ^ = 8, 10 = 8.
- Последнее уравнение смешно. То есть линии не пересекаются, то есть линии параллельны. Пример 3. Нахождение пересечения этих линий 4x + 2y = 8 и 2x + y = 4. Решение этой системы дает: у = 4-2л:, 4л: +2 (4-2л 🙂 = 8, 4л: -ф-8-4л: = 8, 8 = 8. Полученное уравнение всегда верно. Это действительно для любого значения х. Это означает, что две линии пересекаются в каждой точке. Это возможно только тогда, когда они сливаются. Рисунок 17.Обратите внимание, что два уравнения, рассматриваемые в этом примере, эквивалентны и поэтому представляют одну и ту же линию.
Смотрите также:
| Задачи на прямую | Примеры применения линейной функции |
| Общее уравнение прямой. Неявная линейная функция | Парабола |

