Оглавление:


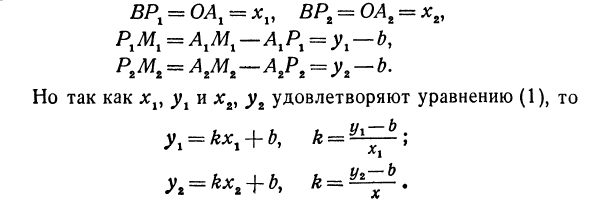






Определение и геометрический смысл
- Определение и геометрический смысл Рассмотрим уравнение с участием двух неизвестных x и y. у = кх + б, (1) Здесь k и b — числа. Этому уравнению удовлетворяет бесконечное число пар чисел x и y. Например, уравнение у = 2х — 6 (*) Следующая пара довольна. х = \ х-2 * = 3 х = 4 х = 5 V17 Y-4 Y-2 y = 0 Y = 2 y = 4 Y = 2 / «17-6 такие как Чтобы найти пару чисел, удовлетворяющих уравнению (), вам нужно дать x любое число и подставить его в уравнение ().
Тогда у получает конкретное число. Например, если n: = 27, y = 2-27-6 = 48. Очевидно, что пара чисел x = 27 и ^ = 48 удовлетворяет формуле (*). Аналогично, в выражении (1) вы можете присвоить x любое числовое значение и получить соответствующее числовое значение для y. В этом уравнении x называется переменной, потому что она может принимать любое число.
Выбор этого числа ничем не ограничен, поэтому x называется независимой переменной или независимой переменной. Людмила Фирмаль
Для y получаются разные значения, но в зависимости от выбранного значения x \, y называется зависимой переменной или функцией. Функция y, определенная уравнением (1), называется линейной функцией. Пример 1. Уравнение >> = 0.5l: вычисляет значение линейной функции, определенной в 3.7, со значениями независимых переменных *, = (), xt = –0.5, xt = –7.6. Если xx = 0, yx = 0,5-0 + 3,7 = 3,7, если 0,5, жж == 0,5 — (- ■ 0,5) +3,7 = 3,45; Если xi = -7,6, ^ 8 = 0,5 — (- 7,6) + 3,7 = -0,1. Если вы получите пару чисел x и y, которые удовлетворяют уравнению (1) как абсцисса и ордината точки, Геометрическое положение этих точек является прямой линией (рисунок 14).
В самом деле, рассмотрим точку B (0, b) и точки Mt (xv yy) и Mt (xуy2 ), координаты которых удовлетворяют уравнению (1). yt = kxt + b9 yy = kxx + b. Указывает на проекцию точки M Mx и Ox thru и Л2 на оси, а ОАх = xv OA2 = xiyAxMx = yvА2Л12 = у2. Из точки B нарисуйте линию, параллельную оси Ox. В этом случае b = OB = AXPX = A2P2. Предположим, что точки B, Mx и M2 не находятся на популярной линии. Соединяя точку B с точками Mx и Mg, получим два прямоугольных треугольника ВРХМХ и ВР2М2.
- BP, = OA, = BPr = 0Ag == xg, P.M ^ A ^ -A.P ^ y-b, Однако, поскольку y, x1 и y2 удовлетворяют уравнению (1), л = + б%Другими словами, Bp; ~ * «Bp, ~ Выражения * и ‘* противоположны Положительная нога в соседний угол / Р1ВМ1 и RgVMg. В результате tg £ PlBMl = 6 и tg / ГР1ВМг = k>, поэтому угол острый, поэтому PlBMl = P2BMV. Это означает, что точки M1Y Mg и B находятся на одной прямой. Однако мы предполагали, что эти точки не находятся на одной прямой.
Следовательно, существует противоречие, которое доказывает, что точки Mx, Mg и B находятся на одной прямой. Угол P1BM1 представлен как. Этот угол образован прямой линией BM1 с положительным направлением оси Ox. Поскольку Mt и M2 — произвольные точки, координаты которых удовлетворяют уравнению (1), можно сделать следующий вывод: Тонер, координаты которого удовлетворяют уравнению (1), отрезает отрезок OV = b на оси Oy Направление оси Ox, которая лежит на линии, которая дает положительные значения, является углом a, таким, что tan a = k. Число b называется начальной ординатой, а число k — коэффициентом угла линии.
Вы можете заключить с предыдущим аргументом. Например, линейная функция y-V —4 определяет линию на координатной плоскости, обрезая сегмент-4 по оси Oy и наклоняя ее относительно оси OX под углом 60 °. tg60 ° = 1 / ~ 3. Если отрезок b на оси Oy обрезан и имеется определенная прямая линия, наклоненная относительно оси OX под углом a (a ^ = 90 °)
Линейная функция от y до kx — \ — b определяет линию на плоскости с начальной ординатой b и угловым коэффициентом k. Людмила Фирмаль
Если касательные, берущие любую абсциссу, равны, то есть только одна точка на указанной линии с этой абсциссой. То есть существует только одна точка для данного x, поэтому существует только одно значение y. Очевидно, имеет место следующее утверждение: прямая, отсекающая отрезок b на оси Oy и касательная которой наклонена к оси Ox под углом, равным числовому значению k}, является линейной функцией y = kx — \ — b Это соответствует.
Поскольку координаты любой точки указанной линии удовлетворяют уравнению (1), уравнение kx + l называется линейным уравнением. Следовательно, линейная функция является линейным уравнением. Пожалуйста, будьте осторожны в особых случаях. 1. Установите b = 0. Другими словами, линейная функция определяется следующим уравнением: у- = кх. (2) Линия, определяемая этим уравнением, проходит через начало координат. Где у пропорционально ху.
То есть х При увеличении (уменьшении) в несколько раз значение u увеличивается (уменьшается) на ту же величину. 2. Пусть =, то есть tga = 0, тогда a = 0. Линейная функция — это уравнение у = б. (3) Это уравнение соответствует прямой линии, параллельной оси Ox, а затем расстоянию b. Исходя из всего, что упомянуто в этом разделе, легко решаются следующие проблемы: Задача 1. Даны баллы A (3, 5) и B (-1, 4). Мне нужно выяснить, находятся ли эти точки на линии в виде уравнения у-2х— 1. (*)
Решения. Если точка находится на прямой линии, ее координаты должны удовлетворять уравнению прямой линии. Поэтому для решения задачи подстановка координат точки A в формулу () дает 5 = 2-3-1. Поскольку это тождество, точка А находится на прямой. Подставляя координаты точки B, получаем 4 = 2 (-1) –1 –3. Это указывает на то, что точка B фне находится на прямой линии. Задача 2. Создать линию с уравнением Y = jX + 3 (*)
Решения. Например, чтобы создать линию, вам нужно знать две точки. Так что дайте х любое значение (например, х = 2) и найдите значение по формуле () 2 + 3 = 4. Следовательно, точка A (2, 4) находится на прямой. Это первая точка. Здесь укажите другое значение для x, например, g = -2, и вычислите y по формуле (). у = -2) + 3 = 2 получается. Точка B (-2, 2) По прямой. Это второй момент. Создайте точки A и B (рисунок 15) и проведите через них прямую линию. Это предпочтительная прямая линия.
Смотрите также:
| Дальнейшие сведения из теории рядов | Основное свойство линейной функции |
| Координаты на плоскости | Задачи на прямую |

