Оглавление:






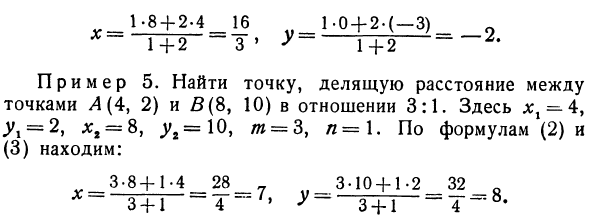
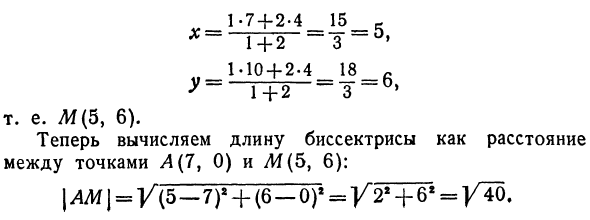



Координаты на плоскости
- На плоскости нарисуйте две взаимно перпендикулярные линии, которые пересекаются в точке O. Для каждой из этих линий установите направление с помощью стрелок (рисунок 7). Установите общую шкалу для обеих линий и выберите точку O для начала координат. Оси координат плоскости определения 1) направление, 2) масштаб, 3) общая опорная точка установлена, перпендикулярны две прямые линии друг с другом.
Одна из осей называется осью Ox или горизонтальной осью, а другая называется осью Oy или осью ординат. Их пересечение называется происхождением. Получить произвольную точку Mu на плоскости, а затем опустить перпендикуляр на осях. То есть найти проекцию на ось. Координаты точки A (вдоль оси Ox) выражаются как lg, а координаты точки B (вдоль оси Oy) выражаются как y. Вот определения: Абсцисса точки определения — это координата проекции на ось Ох.
Проекция на ось Ox представлена буквой A, а проекция на ось Oy представлена буквой B. Людмила Фирмаль
Ордината точки — это координата проекции на ось Oy. Обычно абсцисса точки обозначается буквой x, а ордината — буквой y. Точка M с абсциссой x и ординатой yy определяется следующим образом: Напишите скобку, сначала поместите абсциссу во вторую ординату и разделите эти два числа запятой или точкой с запятой. так На рисунке 7.
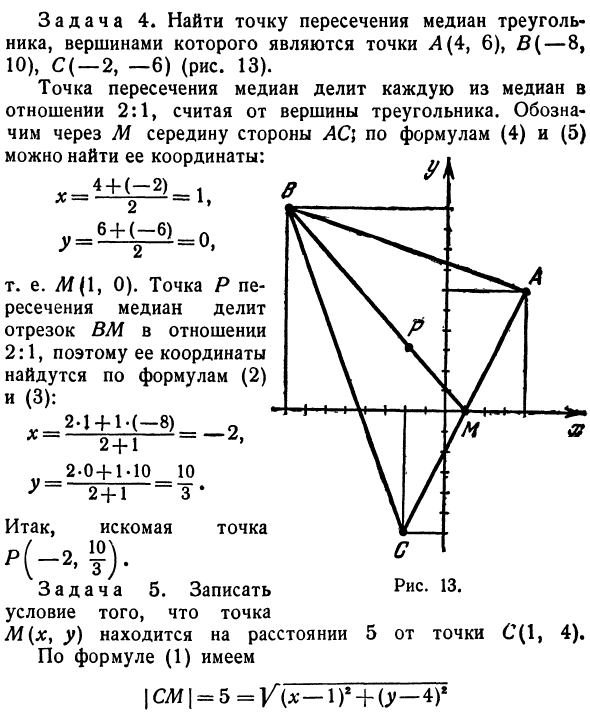
_ 1 -7 + 2-4_15_- 1 + 2-3 ‘ 1 • 10 + 2-4 18, Y = G + 2 = IF = * То есть М (5, 6). Далее длина биссектрисы рассчитывается как расстояние между точками A (7, 0) и M (5, 6). AM | =] / (5-7) 2 + (6-0) 2 = | / * 2 * -j- 6 * = ug40.Задача 4. Найдите пересечение медиан треугольников, вершины которых A (4, 6), B (-8, 10), C {-2, -6) (рис. 13). Медианное пересечение делится на соотношение 2: 1, считая каждую медиану от вершины треугольника.
- Центр боковой стороны динамика обозначен буквой M. Координаты можно найти по уравнениям (4) и (5). То есть М (1, 0). Средняя точка пересечения P делит сегмент VM в соотношении 2: 1, поэтому ее координаты могут быть определены по уравнению (2) (3): 2,1 + б (-8) _ 2 + Т ^ _2-0 + S0_10 2 + 1-3 л Итак, желаемая точка Задача 5. Рисунок 13. Состояние точки M (xy y) находится на расстоянии 5 от точки C (1, 4). Из уравнения (1) \ CM \ = 5 = Y (x- ) r + (y-4) r Или если вы возводите в квадрат обе стороны равенства, ) ”+ (>, _ 4) ‘= 25. (*) Это уравнение является уравнением с двумя неизвестными х и у. То есть координаты точки на расстоянии 5 от точки C удовлетворяют этому уравнению, то есть координаты любой точки, принадлежащей геометрическому расположению точки на расстоянии 5 от точки C.
Следовательно, уравнение (*) можно назвать уравнением окружности с центром в точке C и радиусе 5. В следующей главе мы рассмотрим уравнение с участием двух неизвестных x и y и линию (геометрическое местоположение) с точкой с координатами, которые удовлетворяют этим уравнениям. Практика ч. Я 1. Рассчитайте длину сегмента. Начальная точка сегмента — точка (–3), а конечная точка — точка (–20). 2. Сегмент является положительным или отрицательным, если начало сегмента: 1) Это точка (-I), а конец — точка (+3). 2)
Начало в точке (+14), конец в точке (+8). 3) Вы начинаете с (–5) и заканчиваете (–2)? 3. 2. 4. Найдите расстояние между точками A (0, -4) и B (3, 4). 5. Для A (3, 4) и / 3 (-1, -I) найдите длину отрезка AB. 6. Для Λ (1, 2) и B (7, 8) найдите точку C, которая делит отрезок AB на отношение 2. 7. Найдите точку, которая делит расстояние между точкой P (-3,4) и Q (5,6) пополам. 8. Докажите, что треугольник, вершинами которого являются точки A (1, 2), B (3, 4) и C (-1, 4), является прямоугольником. 9. Найдите среднюю длину треугольника с вершинами в точках A (3, 4), H (-1, 1) и C (0, -3).
Для L (-2) и B (+5) найдите точку, которая делит отрезок AB на отношение Людмила Фирмаль
Таким образом, точечная запись выглядит как M (x, y). Ось координат делит плоскость на четыре части, называемые квадрантами. Первая четверть является частью плоскости, где абсцисса и ордината положительны. Во второй четверти абсцисса отрицательна, а ордината положительна.
В третьем квартале абсцисса и ордината отрицательны, и, наконец, в четвертом квартале абсцисса положительна, а ордината отрицательна (рис. 7). На рисунке 8 показаны точки M1 (5, 2), Mg (-1, 1), LM-1, -3), Zh4 (2, -3). Поскольку абсолютная абсцисса x = OA равна расстоянию точки от оси ординат, поскольку OA = BM (см. Рисунок 7), ордината OB = AM, поэтому точка M от оси абсциссы расстояние. Пример 1. Найти точку P (-4, 2) (рисунок 9). Возьмем точку A на оси Ox с координатой -4 и координатным сегментом OA = -4.
Возьмите точку B на оси Oy Когда координатный сегмент OS = 2, восстановите точки A и B и перпендикуляр от пересечения с осью, и дайте желаемую точку P. в О х м7 \ Рисунок 8.да П в A O X Рисунок 9 Задача 1. Найти расстояние между точками P (xv yy) и Q (* i> Yx). Другими словами, нам нужно найти длину отрезка PQ (рисунок 10). Проекция точки P на ось Ox представлена Av, а ее проекция на ось Oy представлена B%. Проект Q точка на оси Проецирует Ox на Ar и Br на ось Oy. Далее ОАх = хх, ОВх = у> ОАг = х1УОВг = у. Нарисуйте линию, параллельную оси Oxu из точки P, пока она не пересекает линию AtQ в точке K.
Теорема Пифагора дает PQ * = PK * + KQ * (#). Однако RK = AXA „KQ = BxBt> на другой стороне прямоугольника. Кроме того, направленные сегменты AxAg и BxBr равны на основе формулы (3 в § 1) AxAt = OA% -OAx xg — xx; BxBr = OB% Подставляя выражение, полученное в (*), оно получается следующим образом. PQ * = (* i —Xx) r + (A — A) 1 » Где _ I pa \ = Y (xx-xx) w + (ush-yy) \ (1) Другими словами, расстояние между двумя точками равно квадратному корню из суммы квадратов разности координат. Примечание. Поскольку расстояние между двумя точками и длина сегмента всегда положительны, перед квадратным корнем в уравнении (1) используется только знак плюс.
Пример 2. Найти расстояние между точкой P (-2, -1) и Q (2, 2). Используйте уравнение (1) для получения: Пример 3. Найти длину сегмента MNy, если указаны M (8,2) и N (2,10). Используйте уравнение (1) для получения: \ MN \ = W-8) 2+ (10-2) * = 10Задача 2. Если вам известны координаты точек P (xv yy) и Q (x „yy), найдите точку C, которая делит отрезок PQ по n. CQ «» ~~ p •
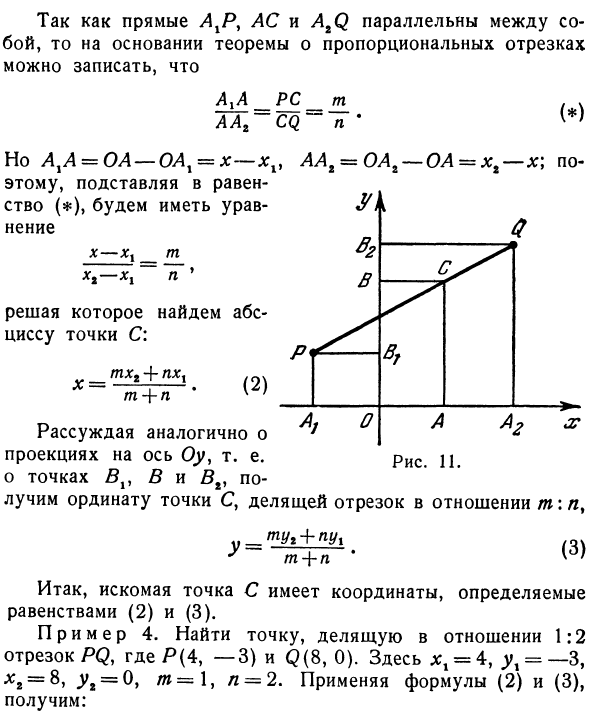
Поскольку линейные сегменты AXR, AC и AtQ пропорциональны друг другу, их можно записать следующим образом на основе теоремы о пропорциональном сегменте. A1A__RS_t_ AA2 CQ ‘ N Однако AxA = OA-OAl = от x до xv AAt = OAg-OA = x1 — x \ Следовательно, подстановка в уравнение (*) дает уравнение. x — xt t p ‘ (2) Решение для нахождения абсциссы точки C: mx ”+ xx X— —LJ-! т + р (3) Аналогично, обсуждая проекцию на ось Oy, то есть точки Bx% B и B%, получаем ординату C, отрезок m \, Y т + р
Таким образом, интересующая точка C имеет координаты, определенные уравнениями (2) и (3). Пример 4. Найти точку, которая разделяет отрезок PQ P (4, -3) и Q (8,0) на соотношение 1: 2. Где ^ = 4, yx = -3, xr = 8y, yy = 0, f = 1, n = 2. Применяя уравнения (2) и (3):Решения. Как и выше, проекция точки P на ось представлена Ar и Bv, проекция точки Q представлена Ar и Br, тогда OAx * = xx% OBl = yv OAg = -xg, OBt = yt (рисунок 11). Кроме того, координаты желаемой точки C представлены x и yy, а проекция на ось представлена A и B. То есть OL = l: OB = y.
1,8 + 2,416 4t_1-0 + 2 «(-3) 1 + 2 3 ‘Y «1 + 2 ~ Пример 5. Найти точку, которая делит расстояние между точками A (4, 2) и 5 (8, 10) на соотношение 3: 1. Где = Yx = 2, i, = 8, j> 2 = 10, i = 3, 2 = 1. Уравнения (2) и (3) показывают, что: _ 3-8 + 1-4 _ 28 _ 3-10 + 1.2 _ 32 Q s + 1 y-s + 1Результаты (из уравнений (2) и (3)). Если точка C делит сегмент PQ пополам, то m = n, поэтому xi + xt Да: -_- 2 1 ts_U1 + Ug 2> (4) (5) То есть центральная абсцисса сегмента равна средней арифметической абсциссе в начале и в конце.
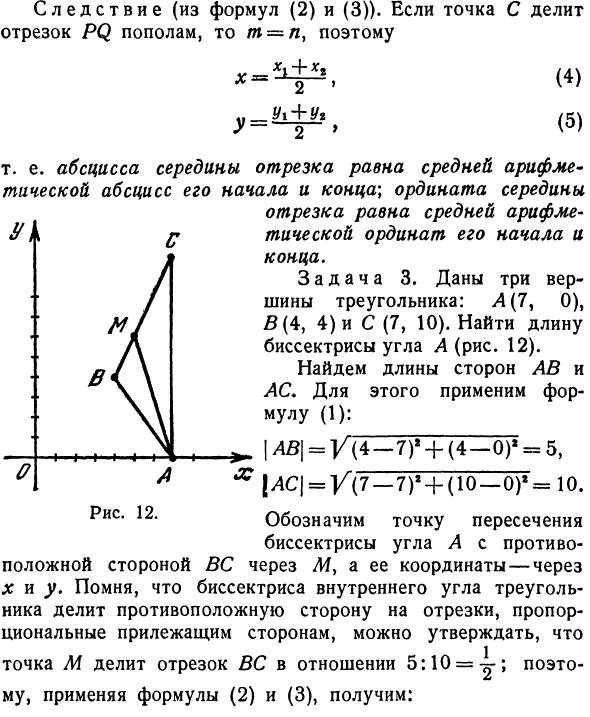
Вертикальный в Сегмент равен средней арифметической ординате начальной и конечной точек. Задача 3. Учитывая три вершины треугольника, A (7, 0), B (4, 4) и C (7, 10). Найдите длину биссектрисы угла A (рисунок 12). Найдите длину сторон AB и AC. ♦ Для этого примените уравнение (1). LA | = / (4-7) ‘+ (4-0)’ = 5 \ AC \ = Y (1-7) e + (10-0) * = 10. Пересечение биссектрисы угла A и противоположной стороны BC обозначено через I, а его координаты обозначены через x и y. Напоминая, что биссектриса внутреннего угла треугольника разделяет противоположную сторону на сегменты, пропорциональные соседним сторонам, можно утверждать, что Точка М делит отрезок BC на соотношение 5:10 = -. Таким образом, применяя уравнения (2) и (3): Рисунок 12.
Смотрите также:
| Криволинейные интегралы | Определение и геометрический смысл |
| Дальнейшие сведения из теории рядов | Основное свойство линейной функции |

