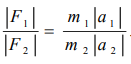Оглавление:


Рассмотрим постановку предмета гидродинамика
Общая постановка по проблемам механики жидкости. Если рассматривать новую жидкость в образовании как ряд материальных частиц которые непрерывно заполняют пространство или возможно его часть, в которых возникают силы гидромеханики для внутреннего технического взаимодействия. Выраженные в идеальной образованной жидкости этим гидродинамическим сильным давлением, то можно сформулировать общую гидродинамическую задачу следующим образом.
Внутренние действующей силы в новой каждой созданной точке и в каждый полученный момент движения технической жидкости, происходит гидродинамическое давление.
Рассмотрим случай несжимаемых и сжимаемых тех. жидкостей в обоих случаях мы сможем рассчитать жидкость, которая будет идеальной и однородной для простоты. Формулировка уравнения движения в форме Лагранжа гидродинамической задачи о вязких неидеальных жидкостях рассматривается в части 2 курса. Движение жидкости в корне отличается от движения жидкости в воде.
Движение жидкости
Свое движение, жидкость не может держать расстояние между своими частицами неизменным. Учитывая движение основного объема жидкости, его можно представить в виде суммы 3-х движений: поступательного и вращательного движений объема жидкости в целом, а также движений различных частиц рассматриваемого объема по отношению друг к другу. При перемещении жидкостей необходимо учитывать массу и силы трения(вязкость). Механика жидкости, используется понятие жидких частиц.Это элементарный объем жидкости, который условно выделяется, и изменение его формы незначительно.Движущиеся частицы жидкости представляют собой кривую, называемую траекторией движения.
Поток жидкости-это движущаяся масса жидкости, которая полностью или частично ограничена поверхностью.Эти поверхности могут быть образованы самой жидкостью на границе раздела фаз,или они могут быть твердыми. Границей случая несжимаемой жидкости течения является стенка трубы, канал, поверхность, по которой течет жидкость, открытая поверхность жидкости.
Из-за малой сжимаемости жидкости, во многих случаях, изменение ее объема может быть полностью проигнорировано.Затем они говорят о несжимаемых жидкостях.Это хорошо используется несжимаемая жидкость, называется предельным случаем сжимаемой жидкости, когда бесконечное сжатие достаточно для создания бесконечно большого давления.
Жидкость, в которой сила внутреннего трения не возникает при ее движении, называется другими словами, идеальная жидкость имеет только нормальное давление, которое однозначно определяется степенью сжатия и температурой жидкости. Идеальная модель жидкости используется, когда скорость изменения деформации жидкости мала. Это уравнение показывает, что когда жидкость находится в равновесии, плотность силы, действующей на единичный объем жидкости, является градиентом скалярной функции.
Это необходимое и достаточное условие для сохранения силы. To уравновешивая жидкость, мы видим, что жидкость требует консервативной силы неконсервативное силовое поле, равновесие невозможно. Из уравнения видно, что в случае механического равновесия давление не зависит от постоянен на любой горизонтальной поверхности.
| Подобия Ньютона: | Числа Фруда: |
| gL*v-i+F | 236 F |
| xrL*v-c+F | 285 F |
| brL*v-f+F | 2376 F |
| trL*v-q+F | 205 F |
| pqL*v-c+F | 234 F |
| osL*vd+F | 328 F |
| isL*v-a+F | 34 F |
| ynL*vc+F | 354 F |
| zeL*v-x+F | 32 F |
| cuL*v-z+F | 35F |
| nwL*v-n+F | 657 F |
| thL*v-m+F | 86 F |
| eaL*vo+F | 21 F |
| nqL*v-a+F | 32 F |
| yuL*vr+F | 54 F |
| neL*v-l+F | 05F |
| xrL*v-c+F | 05 F |
| htL*v-c+F | 83 F |
| rL*v-c+F | 94F |
| wneL*v-b+F | 67 F |
| iuL*v-n+F | 06 F |
| kwL*v-m+F | 24F |
| jyL*v-z+F | 45 F |
| еуL*v-k+F | 543 F |
Горизонтальная поверхность такая же, как и поверхность давления. Именно поэтому свободная поверхность жидкости выравнивается, ведь она находится под постоянным атмосферным давлением. Из 3-го уравнения системы мы видим, что для механического равновесия необходимо, чтобы оно было только функцией. Если зависимость ускорения силы тяжести от широты и долготы незначительна, то плотность изменяется только в зависимости от высоты.