Оглавление:


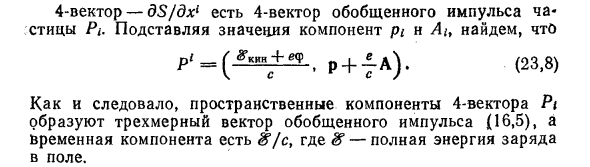

Тензор электромагнитного поля
- Тензор электромагнитного поля. В §17 было выведено уравнение движения заряда в поле. Из функции Лагранжа (16.4), написанной в формате 3D. Получите то же уравнение прямо из действия (16.1) Написано в 4-мерной записи.
Принцип минимального действия чтения б 6S = 6 I [- tf ds — Aidxj) = 0. (23,1) Обратите внимание, что ds = \ Jdxidxr (интегральный предел И б, для краткости опустите следующее): SS = — [(mcdx% d ^ x + -Ai dSxr + -SAi dxL = 0. J и J V DS
два члена целочисленного выражения Готовим частично Людмила Фирмаль
Первые . Кроме того, на первом этапе мы представим 4-ступенчатую Рост dxi / ds = n тогда J (m cdui6xt + -6x ‘1dAi — 6Aidx’ 1 ^ — (rncui + -Ai ^ 6x ‘1 = 0. (23,2) Второе слагаемое в этом уравнении равно нулю.
Изменения в пределах заданных координат. К следующему SAi = Щdxk, dAi = Щdxk, 1 дхк г дхк Таким образом, (McduiSx1 + I5xldxk-dxl5xk) = 0 (/ ^ C dx с dx J ‘ В первом члене dui = ds, во втором и третьем dxg = Д.С. = ульдс Кроме того, в разделе 3 мы обмениваем индекс г И к (это ничего не меняет. К Total).
- тогда / t cd-du-si —— ce (—V ddgA x-gk -gdd-x Ai и ) n 5xlds = 0. Поскольку 6x произвольно, подынтегральное выражение Выражение равно нулю: дуй е (дак даг \ ‘л 92 Зарядка в электромагнитном поле III Вводя обозначение Фик = утка dh1 Daj дхк (23,3)
Этот антисимметричный тензор называется электротензором Магнитное поле Полученное уравнение затем записывается в следующем формате: TC- Д.С. = ~ Исправить. и (23,4) Это уравнение движения заряда в четырехмерной форме. Смысл отдельных составляющих тензора легко понять Заменяет значение A {= (^, -A) в определении (23.3).
Может быть описан в табличном формате с индексом Людмила Фирмаль
результат r = 0,1,2,3 Количество строк и индекс k-столбца: F% k = о случай E „ яйцо Гц -E x -N „ Евросоюз -N х Нью-Гемпшир Эз хорошо о о jpik_ О ■ случай Ep Эз-Н, … -ESG ч з Эй — Время пх Короче можно написать ( Fik = (E, H) я 6): jpik -Е з хорошо -HX о (23.5) = (-Е, Н).
Поэтому электрические компоненты Магнитное поле представляет собой единую 4-тензорную составляющую Электромагнитное поле Если вы посмотрите на трехмерные обозначения, вы можете легко проверить 3 пространственных компонента (r = 1,2,3)
Соотношение (23.4) идентично векторному уравнению движения (17.5), а уравнение для временной составляющей (r = 0) — Бот (17,7). Последнее является результатом уравнения движения. Там Тот факт, что только три из четырех уравнений (23.4) являются независимыми
Вы можете легко обнаружить оба непосредственно, умножив оба ig (23.4), то левая часть равенства исчезает Четыре вектора UI и Dui / DS ортогональность и право Учитывая антисимметрию тензора F ^. При рассмотрении только истинного пути изменения SS Торий, то первое слагаемое в (23.2) также исчезает.
Далее второй член, где рассматривается верхний предел Дайте производную действия как функцию Ордината Вот так Отсюда = циг + = пи + ~ ай. (23,7) OX S C 4D вектор — dS / dx1 является обобщенным 4 вектором Подставляя значения составляющих импульса частиц P, pj и ij, Найди это p i = ^ k и n + eY ^ p + ЈA ^.
Пространственная составляющая 4 вектора Пи выглядит следующим образом Сформировать трехмерный вектор обобщенного импульса (16,5), Компонент времени — ^ / с. Где $ — полная энергия заряда. В поле.
Смотрите также:
| Движение в постоянном однородном магнитном поле | Преобразование Лоренца для поля в физике |
| Движение заряда в постоянных однородных электрическом и магнитном полях | Инварианты поля в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

