Оглавление:



Понятие о функциях Бесселя
Концепция функции Бесселя. Функция Бесселя * широко используется в анализе нелинейных цепей. Прежде чем писать эти общие формулы, помните, что тригонометрические, экспоненциальные и гиперболические функции выражаются в степенных рядах.
- Функция Бесселя является хорошо известным уравнением Бесселя (En 1 dy (p2 \ -Y =) В выражении
аргумент x может быть действительным, чисто мнимым или сложным. Людмила Фирмаль
Значение функции, описанной выше для определенного значения x, может быть определено с использованием ряда выше. Однако на практике это следует определять с помощью графика или таблицы.
Пример 102. Известно, что sin- = 3, sin 30 ° = 0,5. Этот результат получается с использованием уравнения (9.4) I Решение: Заменить формулу (9.4). Вместо -chi ограничить до 6 членов ряда: = 0.5228-0.02355 4-0.0032
- Функция Бесселя с аргументом x представлена Jp (x) Показатель p обозначает порядок функции Бесселя, а общая формула для Jp (x) в форме степенного ряда: (?) ‘(ТГ (if (тГ0! Pl 1) (P4-1)! + 2! (P4-2)! 3! (P4-3)! (9.10)
В дальнейшем чисто мнимые бесселевы функции аргументов являются наиболее важными. Чтобы получить, подставьте / x вместо x, где / = V «-1. (H (f) ‘(?) ■■’ + — ^ + n, < ‘»> SW пример J0 (j4) поиск по формуле (9.11) 2 * 2″ 2e 2 «2’o
Функция Бесселя нулевого порядка Людмила Фирмаль
решение. A (/ 4) = 1 + _ + — + — + + … = 1 + 4 +., 64 256 1024 + + 36 + 576 + 14 400 ‘® 1,3, чисто мнимый аргумент / функция Бесселя первого порядка от x есть x A (/ *) = / ^ — + / (9.12
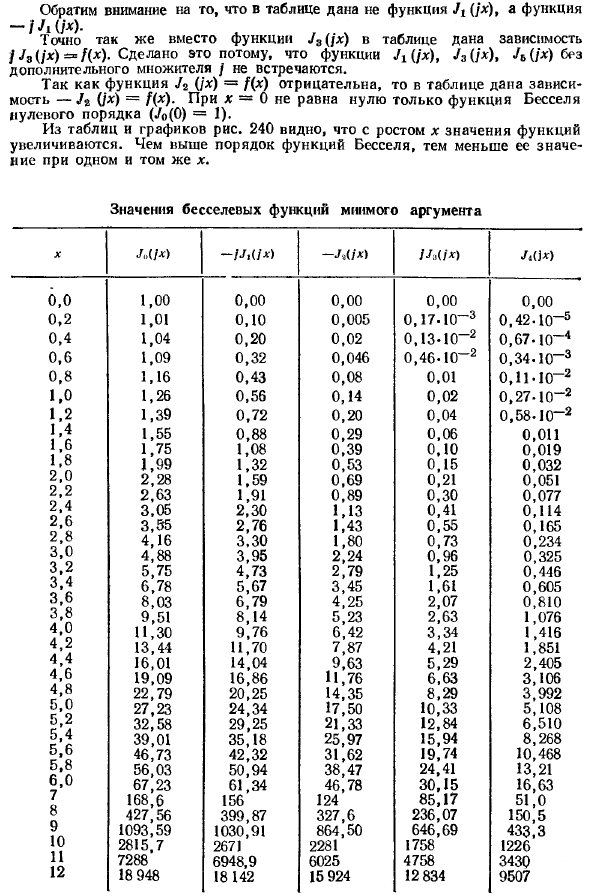
Функции Бесселя и ряды высшего порядка, равные (9J3) чисто мнимого аргумента fx, записываются аналогичным образом: таблица функций Бесселя ниже и кривая на рисунке 240 из них Таблица не является функцией Jt (jx), но вместо функции-Л ((/ *) •
функция J3 (/ x) зависимость представляет собой таблицу / 78 (/ x ) / (X), что сделано потому, что функция A (/ x), AO *) »A (M) не возникает без дополнительного множителя /. Функция A (/ *) = Поскольку / (*) отрицательно, зависимость задается как Таблица-J2 (jx) = f (x).
Если x = 0, только маркированная функция Бесселя ненулевая (A> (0) = 1). Из таблицы и графика видно, что значение функции увеличивается с увеличением на рисунке 240х. Чем выше порядок функции Бесселя, тем меньше значение того же x.
Значение функции Бесселя мнимого аргумента XL (/ x) —L (/ *> JJAix) / «(! *) 0,0 1,00 0,00 0,00 0,00 0,00 0,2 1,01 0, 10 0,005 0,17,10—3 0,42-10-5 0,4 1,04 0,20 0,02 0,13-10 до 2 0,67-U-4 0,0 1,09 0,32 0,046 0,46 -10 до 2 0,34,10_3 0,8 1,16 0,43 0,08 0,01 0,1blO-2 1,0 1,26 0,56 0,14 0,02 0,27-10 “2 1, 2 1,39 0,72 0,20 0,04 0,58-10-2 1,4 1,55 0,88 0,29 0,06 0,011 1,6 1,75 1,08 0,39 0 10 0,019
1,8 1,99 1,32 0,53 0,15 0,032 2,0 2,28 1,59 0,69 0,21 0,051 2,2 2,63 1,91 0,80 0,30 0,077 2,4 3,05 2,30 1,13 0,41 0,11 2,6 3,55 2,76 1,43 0,55 0,165 2,8 4,16 3,30 1,80 0,73 0,234 3 0 4,88 3,95 2,24 0,96 0,325 3,2 5,75 4,73,79 1,25 0,446 3,4 6,78 5,67 3,61 1,65 0,60 3,6 8,03 6,79 4,25 2,07 0,810 3,8 9,51 8,14 3,23 2,63 1,07 6,0 11,30 9,76 6,42 3,34 1,416 4,2 13,4 44,70 7,87 4,21 1,8,1 4,4 16,01
14,04 9,63 5,29 2,40 4,6 19,09 16,86 11,76 6,63 3,106 4,8 22,79 20, 25 14,35 8,29 3,992 5,2 27,23 24,34 17,50 10,33 5,108 32,58 29,25 21,33 12,84 6,510 5,4 39, 01 35,18 25,97 15,94 8,2 68 5,6 г * 46,73 42,32 31,62 19,74 10,468 5,8 56,03 50,94 38,47 24,41 13,21 6,0 67,23 61,34 46,78 30,15 16,63 7 168,6 156 124
85,17,0,0 8 427,56 399,87 327,6 236,07 150,5 9 1093,59 1030,91 864,50 694 1 3430 12 18 948 18 142 15 924 12 834 9507
Смотрите также:

