Оглавление:





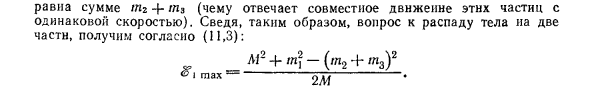

Распад частиц в физике
- Распад частиц. Рассмотрим спонтанный коллапс объекта с массой М на Две части масс ми и м2. Закон сохранения энергии при коллапсе применяется к системе отсчета, где тело отдыхает, 1) M = $ 10 + ^ 20? (11.1) Где Ao и ^ 20 — энергия летной части.
После $ \ §> > Для 7774 и S20> m 2 уравнение (11.1) может быть выполнено только в том случае, если M> 7774+ 777.2. Наоборот, при М <777,1+ тело устойчиво (с точки зрения этого затухания) и не распадается естественным путем.
С законом сохранения энергии при коллапсе Удовлетворен закон сохранения импульса Людмила Фирмаль
Чтобы выполнить затухание, в этом случае необходимо информировать тело об энергии, по меньшей мере, равной его «энергии связи» (7774+ 777,2-М). . То есть, как и начальный импульс тела, полный импульс полетной части равен нулю: рю + P20-0. Следовательно, p20 = o> или ^ 10-м 1 — <* 20 ~ м 2- (11,2) Для уравнений (11.1) и (11.2) энергия летной части определяется однозначно.
г _ М2 + т \ -мл ^ _ М2-мл + мл 10 _ 2м -20-2МВ * J В некотором смысле обратное является вычислительной проблемой Полная энергия M двух сталкивающихся частиц в системе отсчета с суммарным импульсом, равным нулю (или, для краткости, инерциальная система центров или «система c»).
- Этот количественный расчет обеспечивает основу для определения потенциала для различных процессов неупругих столкновений, связанных с изменением состояния сталкивающихся частиц или «рождением» новых частиц. Каждый такой процесс происходит только при условии, что общая масса всех «продуктов реакции» не превышает М.
Пусть это будет оригинальная (или лабораторная) система, как говорится Для справки: частицы с массой mi и энергией сталкиваются со стационарными частицами с массой m2. Полная энергия обеих частиц равна полному импульсу p = pi + P2 = Pb. : Это скорость перемещения системы g ^ относительно лабораторной системы (систем).
вы можете конвертировать из одной системы отсчета в другую Людмила Фирмаль
Однако нет необходимости определять целевую массу М. На самом деле, . Вместо этого уравнение (9.6) можно использовать напрямую. Это уравнение может быть применено к сложным системам отдельно от каждой частицы.
Поэтому мы имеем Задача 1. Частица, движущаяся со скоростью V, на лету коллапсирует на две частицы. Определите связь между последним начальным углом и энергией. Решения. где $ o — энергия одной из частиц распада c-системы (т. е. S’io или (11.3) $ 20), $ — энергия той же частицы в l-системе, а c — угол выхода l-системы. (Для направления V).
Используйте Формула преобразования (9.15) -777/2 Откуда M 2 = S 2-p2 = ($ \ + m2) 2- [S2-m ) M 2 = m \ + 7mt | + 2m 2 (? I- (11,5) Откуда N потому что в = ———. W V) или 2 (если vq po / So = vo, точка A находится вне эллипса (рис. 3-6) и двух для заданного угла (и энергии S) вектора p Рисунок 3 Разные значения. В этом случае структура также показывает, что угол может принимать только значения, которые не превышают определенного максимального значения (соответствующего положению вектора p, касающемуся) Эллипс).
Значение max легче всего определить аналитически из условия, что дискриминант квадратного уравнения (2) исчезает и становится равным следующему условию. , И ПОВТ ^ V * см 6> м х х = ——————— ————. милливольт 2. Найти распределение энергии распадающихся частиц с помощью электронной системы. Решения. В r ^ -системе распадающиеся частицы изотропно распределены в направлении. Другими словами, отношение количества частиц в элементе телесного угла doo = = 2 г с.
Энергия g-системы связана с количеством, связанным с g-системой. отношение Выполнить значения между Сп-уро ^ $ о + уро V i-V2 и V i-V2 ‘ Через выражение | dcos # o | d <# ‘получить единичное нормированное распределение Энергетическое соотношение (каждый из двух типов распадающихся частиц): d N = -i — h / l-V 2 dS. 2vp0 3.
Определить диапазон возможных значений для .d-системы Угол между двумя коллапсирующими частицами во время распада до (угол расширения) Две одинаковые частицы. Решения. В r ^ -системе частицы рассеиваются друг против друга Неправильное направление, т.е. vu = tg- # 2 0 = отношение между углами Системы q и l приведены в соответствии с уравнением (5.4).
, Q _ vq cos in + V -Vo cos in + V C s 1 w0 sin ^ oVl-V2 ′ C s 2 ”V0 sin6> 0 \ / 1-V2 (В этом случае vio = ^ 2 0 = vo). Желаемый угол развертывания O = in \ + # 2 и Это можно получить с помощью простого расчета ct 0 = V2-Vp + V2vp sin2 Ap Cg 2Vv0Vl-V2 sin 0O Это экстремальное изучение выражения приводит к следующему Возможное значение вала
Если V / l-V2 ^ <0 <7r; Во- Если vo \ A-vl 0 <0 <2 a r c t g y / 1-V2 ^ < 4. Найти угловое распределение распадающихся частиц в электронной системе Масса равна нулю. Решения. Соотношение между системой детали c и начальным углом системы .d ts с m = 0 дается в соответствии с уравнением (5.6). n cos v-V потому что в = —————. 1-V курс Подстановка этого уравнения в уравнение (1) для задачи 2 дает dN = (l-y2) до 4 тг (1-VcosO) 2 5.
Найти распределение угла расширения l-системы при затухании Две частицы с массой, равной нулю. Решения. d-система bi, начальный угол 62 и соотношение углов # 1 0 = Oo, # 2 0 = 7r-r ^ -Система # 0 определяется уравнением (5.6). О углу расширения 0 = в \ + O2 2V2-1-V2 cos2 ~ cos b = 1-V cos2 in И обратно: n 1-V 2 + 2 0 = W l- ^ c t g
Подстановка этого уравнения в уравнение (1) для задачи 2 дает 1-V2 до дн = 16тВ sin3 (0/2) с / V2-cos2 (0/2) Угол 0 составляет от 7 г до 0 минут = 2 arccos V. 6. Определите одну из самых высоких энергий Коллапсируют частицы, в то время как масса М стационарных частиц разрушается в Частицы ми, м2, м3. Решения. Particle mi system Две другие частицы m2 и m3 имеют наименьшую возможную массу.
Последнее соответствует общей м2 + сз (движения этих суставов Частицы с одинаковой скоростью). Таким образом, уменьшая проблему коллапса Разделите тело на две части и получите согласно (11.3) И максимум = [м2 + мл- (t2 + t3) 2] / (2М).
Смотрите также:
| Энергия и импульс в физике | Инвариантное сечение |
| Преобразование функции распределения | Упругие столкновения частиц |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

