Оглавление:
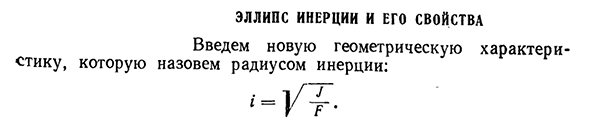



Эллипс инерции и его свойства
- Инерционный эллипс и его характеристики Введение нового геометрического свойства, называемого радиусом инерции: На всех 170 фигурах оси OU и Oz предполагаются главными центральными осями. Запишем представление момента инерции для оси, наклоненной под углом к главной оси J u-J g cos2a + J y sin2a *.
Разделив все члены на F, получим iu-cos2 и 4-i2y sin2a (6.8). Создайте эллипс на осях координат и возьмите половину оси инерции фигуры. В этом случае вдоль оси унции радиус инерции 1G откладывается на радиус i радиусов Y и оси OU соответственно. Композиция этого эллипса выглядит следующим образом V> g + 4- =! • (6,9)
Этот эллипс (рис. 162) называется эллипсом инерции на диаграмме. Давайте Людмила Фирмаль
напишем касательное уравнение для эллипса Ооо, о, gg0 2 + = 1, (6.10) 1G1U Это делается параллельно оси OI. (Где 0 и G0 — координаты точки касания.) Затем Oi находит расстояние между касательной и осью, вы можете увидеть это на чертеже. H-Y G Cos A-4-G о грехе а. Делим все члены на h, история * Центробежный момент относительно шпинделя равен нулю. WO COS a, L + z0 sin a ч ~ 1. (6.11) Сравнивая уравнения (6.10) и (6.11), y COS a g sin a ii2-h9 два ч ч ч ‘ 180 миль
i2i2cos2a sin2a A2 Если мы теперь назначим ценное значение, мы будем в уравнении Инерционный эллипс. — i2cos2a Нет. , Мне 2 Y sin2a + Откуда A2 = i2cos2a + sin2a i2. Сравнивая полученную зависимость с уравнением (6.8), можно видеть, что значение h численно равно
- радиусу инерции относительно оси наклона. Используя установленные свойства инерционного эллипса, вы можете графически определить момент инерции относительно любой оси, проходящей через начало координат. Для этого достаточно нарисовать касательную на эллипсе, параллельном этой оси, и
измерить кратчайшее расстояние между касательной и осью. Это расстояние h равно радиусу инерции рассматриваемой оси. Можно ли найти моменты инерции с помощью равенства = h? F. Если моменты инерции относительно двух главных осей равны, эллипс инерции меняется на окружность.
Это указывает на то, что моменты инерции Людмила Фирмаль
для всех осей, проходящих через центр тяжести, равны друг другу. Для такого сечения все оси являются главными. К таким разделам относятся круги, кольца, квадраты и т. Д.
Смотрите также:

