Оглавление:




Зависимость между моментами инерции при повороте осей. главные оси и главные моменты инерции
- Связь между моментами инерции При вращении вала. Главный топор и главный Момент инерции Найдите моменты инерции для осей OI и Ov и поверните их на угол a относительно системы исходных осей (рис. 158). Давайте выберем произвольную площадку
dF и представим координаты на новых осях через координаты старых осей: Укажите. г Найти момент инерции относительно оси OI: Ja- [v2dF = J (cos a — z sin a) 2dF = cos2a J y2dF + 4-sin2a J z2d F-2sinacosa j yzdF. J y2dF = JZ, J z2dF = J y t J zydF = Jz y, прибудете «/» =
Jz cos2a + sin2 -J2y грех 2а. Аналогично Jv = z sin2a + Jy cos2a + Jzy sin2a. (6.4) (6,4 ‘) Для Людмила Фирмаль
176 центробежного момента инерции, «7cg, = (z / cosa-z sin a) (y sin a4-z cos a) dF = sin a cos y2d F — F или (6 Таким образом, зная момент инерции относительно двух взаимно перпендикулярных осей и момент инерции массы для этих осей, любая ось проходит через одну и ту же точку Интересно отметить, что добавление двух уравнений
(6.4) и (6.4 ‘) дает уже известное соотношение из 47 J U J V J Z J u ‘ Уравнение (6.4) показывает, что величина момента инерции для любой оси зависит от угла оси. Очевидно, вы можете найти значение угла 0, когда момент инерции достигает предельного значения. Чтобы определить экстремальное значение, первая производная уравнения (6.4) устанавливается равной нулю, и a = a0: = — 2Jz cos a e sin ae- | -2 </ y sinae cose-2Jzy cos2ae = 0 или (Jz — J y) sin2a0 + 2Jzy cos2a0 = 0, Откуда
- (6.6)) Полученная формула дает два значения угла a 0: == a ‘+ 90 °, поэтому существуют две взаимно перпендикулярные оси относительно момента инерции, имеющие экстремальные значения. Оси называются главными осями инерции, а момент инерции относительно этих осей называется главным моментом инерции. Детальные исследования показали, что для одной из основных осей инерции момент инерции имеет максимум, а для другой — минимум. Сравнивая уравнения AA (3.5) и J и (6.4), TA (3.6) и j uv (6.5), а также уравнения (6.6) и (3.12), задача нахождения основного момента
инерции математически одинакова. Напряжение 177 головок. Исходя из этого, мы не будем повторять все выводы, а ограничимся конечным результатом. Основной момент уравнения инерции записывается по аналогии с уравнением (26), полученным в §3.13 для главного напряжения: (6.7) Из уравнения (6.7) видно, что величина основного момента инерции напрямую определяется моментом инерции относительно осей Oz и Oh. Поэтому их можно определить, не зная положения самого шпинделя. В дополнение к уравнению
(6.6), вы можете видеть, что положение шпинделя можно найти по моментам инерции / шаха и J мин. Мы не даем формулу вывода, Людмила Фирмаль
которая позволяет найти угол между осью унции и главной осью и A2: 7zy J u j Shah 7zy J y-J min Угол определяет положение оси, где момент инерции становится Jmax, и определяет угол A2-Jmin. Исследование напряженного состояния показало нулевой касательный стресс на главном участке. Аналогично, здесь можно показать, что инерционный момент инерции относительно главной оси инерции равен нулю. Если этот факт легко доказать, уравнение (6.6) заменяет угол a, который заменяет значение угла A0, определенного в уравнении (6.5). Условие равного нулю центробежного момента инерции часто используется для определения положения главной оси инерции. Например, для симметричной фигуры ось симметрии является главной осью. Фактически, мы вычислим основные
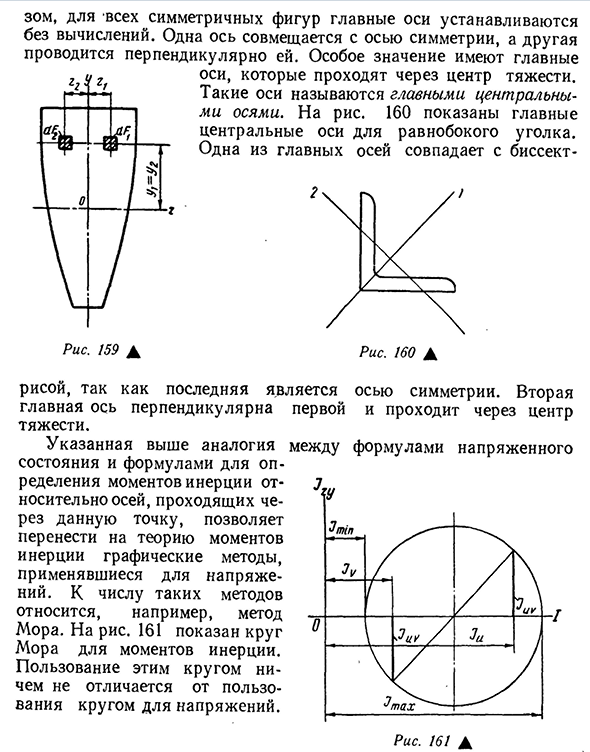
моменты инерции двух одинаковых симметрично расположенных базовых узлов в двух половинах и на равном расстоянии от оси симметрии Op, получим: left Право на точку dJzy = dfiziht, dJzy = d F ^ y * Однако, если dF {= dF2 и z2 = -zit2-y для симметрии, сумма двух основных моментов инерции равна нулю, поэтому инерция Jzy всего сечения Морм обра- Для 178zom, все симметричные формы, главная ось задается без расчета. Одна ось совмещена с осью симметрии, а другая ось удерживается перпендикулярно ей. Особое значение имеет шпиндель, который проходит через центр тяжести. Такая ось
называется главной центральной осью. Для риса. 160 обозначает основную центральную ось угла равнобедренного треугольника. Одна из осей шпинделя совпадает с биссектрисой Последняя является осью симметрии, поэтому рис. Второй шпиндель является первым вертикальным и проходит через центр тяжести. Приведенная выше аналогия между формулой напряженного состояния и формулой, определяющей момент инерции относительно оси, проходящей через эту точку, относится к теории момента инерции, используемой для напряжения. Он включен. Для риса. 161 показывает круг молей для момента инерции. Использование этого круга ничем не отличается от использования круга стресса. Рис 161а
Смотрите также:
| Моменты инерции простейших фигур | Эллипс инерции и его свойства |
| Зависимость между моментами инерции относительно параллельных осей | Вычисление моментов инерции сложных фигур |

