Оглавление:




Моменты инерции простейших фигур
- Простейшее количество моментов инерции Вычисление момента инерции некоторых основных фигур можно выполнить путем интегрирования в соответствии с общим выражением, приведенным
в § 47. Давайте рассмотрим некоторые из наиболее распространенных форм. P R i m g u l l n I K. Сначала давайте найдем момент инерции относительно центральной оси Oz (рис. 153): J2 = f y2dF. F
Духовно разделите прямоугольник на основные области с линиями, Людмила Фирмаль
параллельными оси Oz. Как показано на рисунке, площадь одного произвольного элемента. 153 определяется равенством dF-bdy. Даю 171 ¢ два Jz = B J y2dy = h два Точно так же вы можете рассчитать момент инерции для другой оси, которая проходит через центр тяжести: t_Afc3 u12 * Для оси, проходящей через базу, имеем = b J y \ d yx = Broadcast Как хорошо j_hb3 Давайте посмотрим на моменты центробежной инерции относительно этих осей. Выберите, как и в
предыдущем случае, ширину прямоугольной полосы b и высоту dy в качестве базовой платформы (см. Рисунок 153), находим час Jtivt = [yi ^ dF = J-y yibdyt = F- F Broadcast T R e y g o l l n I K. Рассчитайте момент инерции относительно центральной оси Oz. Ширина основной области на рисунке заштрихована. 154, определяется по сходству
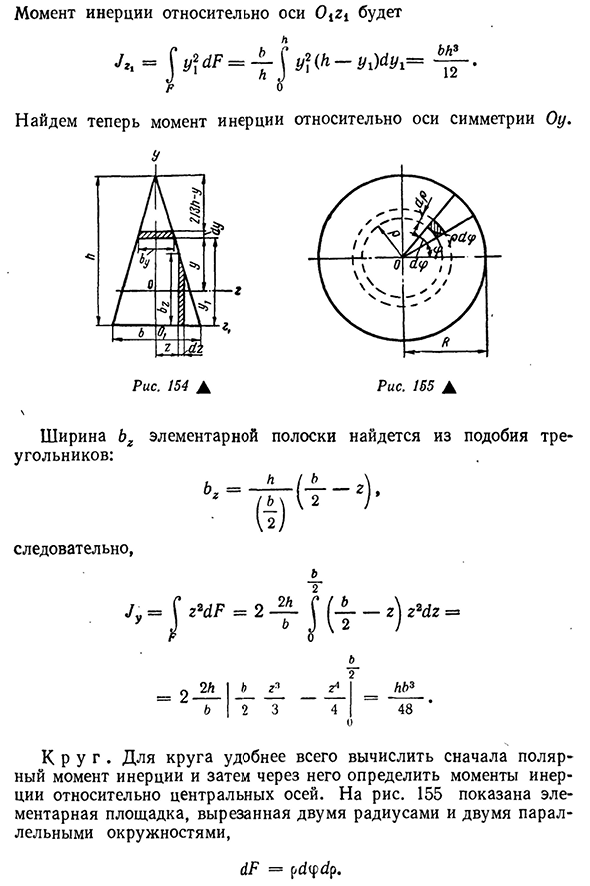
- треугольников: Подставляя это уравнение в интеграл, y2dF = (‘z / 2F_A три три Относительная ось Ot Zi для момента инерции равна Y * (h-yjd y * = описание bh3unit в списках двенадцать Теперь мы находим моменты инерции относительно оси симметрии Огайо. Ширина основной полосы определяется по сходству треугольника: Таким
образом, Для K R u g кругов наиболее удобно сначала вычислить полярный момент инерции, а затем через него определить момент инерции относительно центральной оси. Для риса. 155 показывает основную область, разрезанную двумя радиусами и двумя параллельными окружностями, dF = pdtpt / p. Целое квадратное интегрирование заменяется двойной интеграцией:
Двуосный момент л /? 4 4 Учитывая, что полюс инерции g равен сумме моментов, Людмила Фирмаль
получаем j-J — — — К о л л к о. Момент инерции числа (рис. 156) можно найти как разность моментов инерции двух окружностей: внешнего и внутреннего. Момент инерции полярности y == 2D1_D. = D (I * _g4). P2 2 2 Осевой момент инерции
Смотрите также:

