Оглавление:


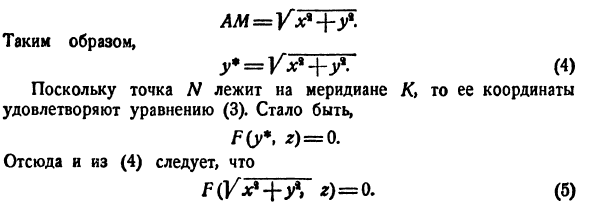

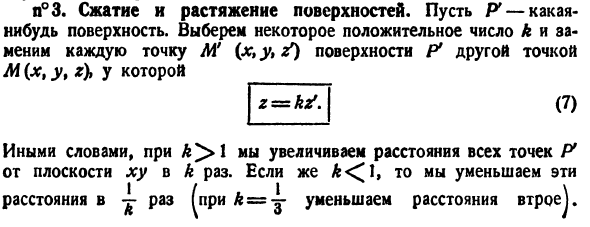




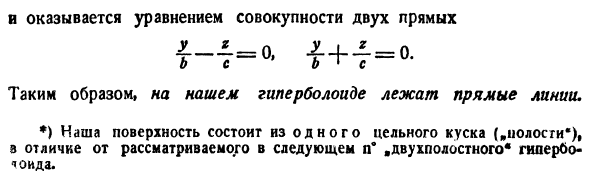







Поверхности 2-го порядка
- Квадрическая поверхность n ° 1. Цилиндрическая поверхность. В этом разделе мы рассмотрим квадратичную поверхность, то есть поверхность с квадратным уравнением. Самым простым из них является так называемая вторичная цилиндрическая поверхность, начиная с этого. Поместите прямую K в плоскость xy (Рисунок 309). Нарисуйте линию, которая проходит через каждую точку K параллельно оси Oz.
Вышеуказанная линия называется генератором поверхности P, а исходная линия K называется ее направляющей. Руководство К уравнение F (xty) = 0. (1) Возьмем любую точку M (x, y, z) из P. Это в каком-то образовании. Если N является пересечением этого генератора и плоскости xy, N находится на линии K, и координаты N должны удовлетворять уравнению (1). Однако ясно, что точка N имеет ту же абсциссу x и ординату y, что и точка M. Следовательно, эти абсциссы и ординаты (точка M ) удовлетворяют уравнению (1). Поскольку M — любая точка на поверхности P, (1) является уравнением для этой поверхности.
Эти наборы линий образуют поверхность P, называемую цилиндром P. Людмила Фирмаль
Вы можете видеть, что уравнение для цилиндрической поверхности с генератором, параллельным оси Oz, не включает в себя координату z (которая соответствует направляющему уравнению). Особенно, когда гидом является эллипс Множество точек на плоскости xy, где x и y удовлетворяют уравнению (13) б — Рассматриваемый раздел Эллипсоид с плоскостью z = h проецируется точно на плоскость xy с результирующим эллипсом и без искажений.
n ° B. Один гиперболоид. Подумай о гиперболе ТГ-1. Лежа на плоскости у Поверните вокруг оси Oz9, чтобы получить поверхность * F I U Рисунок 313. = 1 Это называется одиночным *) вращающимся гиперболоидом. Когда этот гиперболоид растягивается k раз в направлении оси Ox, он достигает общего гиперболоида с одной полостью. Y ‘ T (14) _4. 8 секунд (15)
Для краткости установите bk = a. Из процесса получения этой поверхности ясно, что она имеет форму, показанную на рисунке 1. 313. Сечение гиперболоида с плоскостью z = h является эллипсом, а сечение с плоскостью x = ((| h \ a, обратное также верно. Если | L | = a, то (15) принимает вид = о И оказалось, что это уравнение комбинации двух линий Б с б с Следовательно, прямая находится на гиперболоиде. *) Наша поверхность — это следующая половина двуногого * гипербо- Да с чо.
- Через любую точку гиперболоида вы можете видеть, что две линии полностью лежат на гиперболоиде. На самом деле, пусть M (x9, y9, r0) — любая точка в иерархии (14). тогда xh V * z1 l- Uy — I „1-g-i-: t- ‘» Откуда _ 1 Wo A1 c1 ~ 1 «» или Put хо1 £ оас = т. тогда В связи с (16) d с l \ l + b) ‘ Таким образом, точка M является прямой линией, которая является пересечением двух плоскостей. (Р) И м \ б / *
Однако число (xty, z), которое удовлетворяет уравнению (17), явно удовлетворяет уравнению (14), являющемуся результатом умножения уравнения (17), поэтому эта прямая находится полностью на гиперболоиде. Поэтому мы нашли линию, которая прошла *) M и была полностью на гиперболе. Другая строка с этими свойствами становится строкой Т + 7-М). + <18>
Где m выбрано так, что прямая (18) проходит через M. Поскольку мы хотим подчеркнуть эту ситуацию, этот гиперболоид называется линейным Поверхность и прямолинейный гиперболический генератор прямой линии обсуждались выше. № 6. 2-полый гиперболоид.
Следовательно, один гиперболоид подобен прямой линии. Людмила Фирмаль
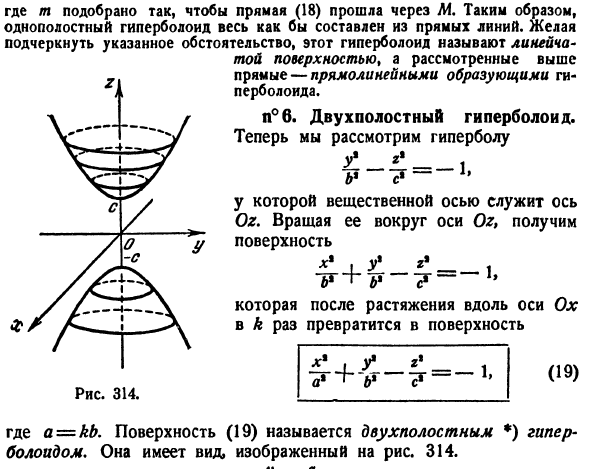
Давайте посмотрим на гиперболу _ 1. Ось Oz является реальной осью. Поверните вокруг оси Oz, чтобы получить поверхность После растяжения k раз вдоль оси Ox, он становится поверхностью Рисунок 314. LU * _, Где а = кб. Поверхность (19) называется гиперболоидом из двух листов. Он имеет форму, показанную на рисунке. 314.
№ 7 Кукуруза. Если линия вращается вокруг оси Oz, Результирующее уравнение конуса является zj ^ Рисунок 315. или ± yx * 2 б-с ^, 0 * до Y * (20) В результате растяжения вдоль оси Ox на коэффициент k этот конус (или вращающийся конус) превращается в общий конус степени 2 z — o Как показано на рисунке 315. Разрез по плоскости z = h — это эллипс, а плоскость; = (или y = h) — гипербола.
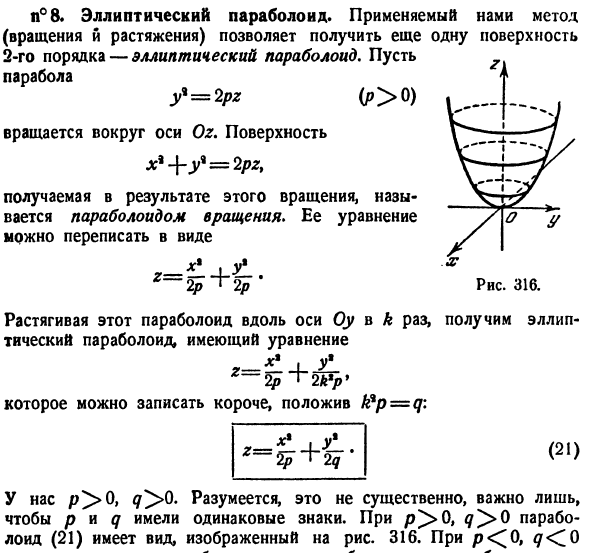
8 ° овальный параболоид. В зависимости от используемого метода (вращение и расширение / сжатие), вы можете получить другой квадратично-эллипсоидный параболоид. Давай параболу Y = 2 / * (,> 0) Вращается вокруг оси Оз. Поверхность x * y * = 2pzt То, что происходит от этого вращения, называется параболоидом вращения. Уравнение можно переписать в виде х%. в
Если этот параболоид растягивают k раз вдоль оси Oy, получается эллиптический параболоид со следующим уравнением. 2p ‘2k * p * Рисунок 316. Вы можете написать коротко, установив k * p = q: (21) z — ** 4U Есть 0 и 0. Конечно, это не обязательно. Важно, чтобы p и q имели один и тот же знак. Когда 0 и q> 0, параболоид (21) имеет форму, показанную на фигуре. 316.Если <7 <C0
Параболоид, как показано на рисунке. 317. Рисунок 317. № 9 Гиперболический параболоид. В заключение рассмотрим квадратичную поверхность, которая не принадлежит ни количеству цилиндров, ни числу граней, полученных методом вращения и растяжения. Эта поверхность называется гиперболическим параболоидом и задается уравнением (22) * ~ 2p 2q * 0, О (или 0, <7 <0). Чтобы распознать форму этой поверхности, пересекайте ее с плоскостью хх. Очевидно, вы должны указать y = 0 для этого. В результате вы получите следующую строку.
Эта парабола симметрична относительно оси Og и имеет вершину в начале координат. Из 0 парабола (23) находится в полуплоскости r ^ 0. Теперь рассмотрим сечение поверхности с плоскостью x = h. Координаты всех точек в этом разделе удовлетворяют уравнению L * VF <24> Поскольку координата xt не попадает в это соотношение, (24) является уравнением для цилиндрической поверхности с генератором, параллельным оси Ox.
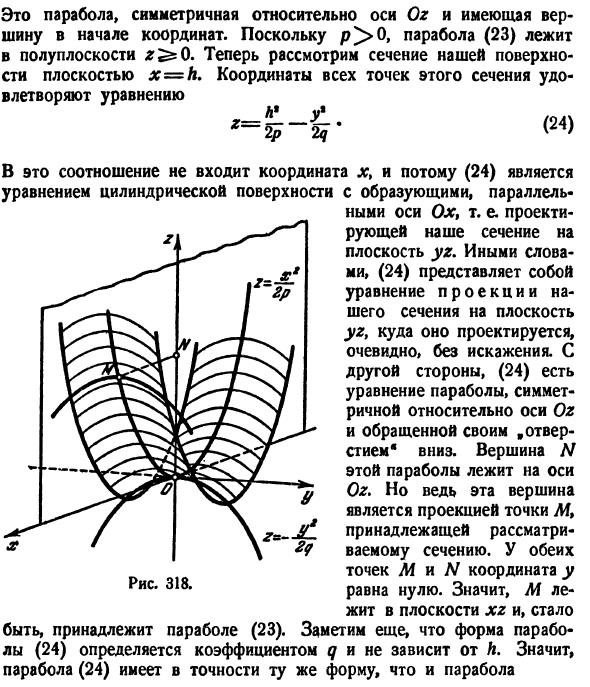
Другими словами, спроецируйте сечение на плоскость y. Другими словами, (24) — это уравнение для проекции сечения на плоскость yy, явно проецируемое без искажений. С другой стороны, (24) является параболическим уравнением, которое симметрично относительно оси Og и обращено «вниз» к отверстию. Вершина N этой параболы находится на оси Og, но эта вершина является проекцией точки Af, принадлежащей целевому сечению.
Координата N на рисунке 318 равна нулю. То есть М Поскольку он существует в плоскости xy, он принадлежит параболе (23). Также отметим, что форма параболы (24) определяется фактором q и не зависит от L. Таким образом, парабола (24) имеет точно такую же форму, что и парабола.
Это участок поверхности на плоскости. Чтобы сравнить все вышесказанное, чтобы получить параболоид (22), переместите параболоид (25) так, чтобы плоскость была параллельна плоскости yy, а вершина Вы можете видеть, что вам нужно скользить по параболе (23). Таким образом, гиперболический параболоид имеет форму, показанную на рисунке 5. 318. Бипараболическая поверхность является доминирующей, как простой гиперболоид. То есть он состоит из прямых линий.
Соответствующая цилиндрическая поверхность называется эллиптическим цилиндром, а (2) является уравнением. Вы можете видеть, что эта поверхность квадратична. Точно так же мы достигаем параболического цилиндра y = 2px и гиперболический цилиндр Параболическая точка — это две линии, которые полностью находятся на параболоиде.
Чтобы доказать это, возьмем точку M (g0, y09 g0) на параболоиде (22). Для нее 0% 2g (уТр ^ УЬ) \ УЬУШ Дай мне U2r U 2q тогда (* 0, 1 \ V’2P Легко увидеть линии Я Х Х. у UTR-у? rt ‘t [y + ushch (26) Пройдите через M (q0, y0, z0). С другой стороны, для tf 0 уравнение (26) можно умножить для уменьшения результата, а для π = 0 уравнение (26) —7 = = °> z = 0 (27) U2r U2d Числовые значения (π, y, r), которые удовлетворяют соотношению (27), также удовлетворяют уравнению (22). Другая линия, проходящая через M (x0, y9, z0) Быть довольным м одевание (х0,:
Есть капуста (22) на параболоиде, прямо где V9 CA Линии (26) и (2S) называются параболическими генераторами (22). Это также квадратичные поверхности. Вообще говоря, цилиндрическая поверхность не обязательно является вторичной поверхностью. Например, поверхность кубического цилиндра соответствует уравнению y = x3, а уравнение sinjc не является алгеброй, поэтому синус-цилиндр * y = sin * не имеет определенного порядка. № 2. Уравнение поверхности вращения. Некоторые квадратные поверхности находятся в так называемых криволинейных поверхностях Вращение.
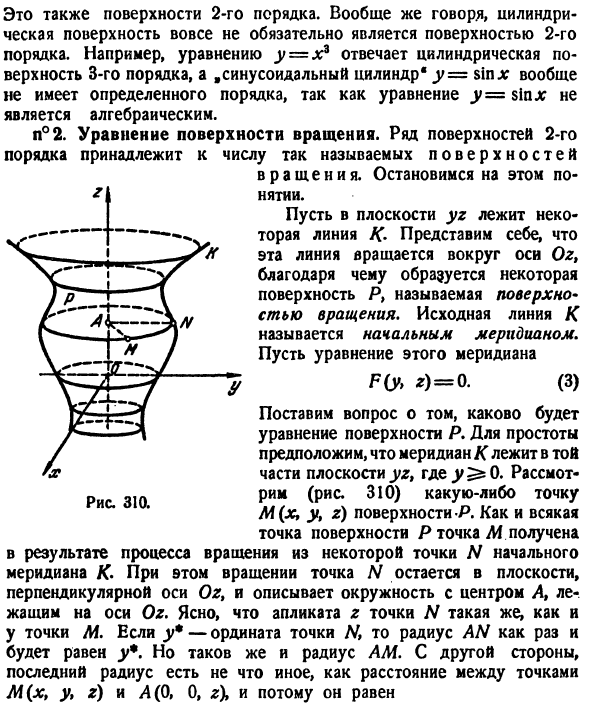
Давайте внимательнее посмотрим на эту концепцию. Представьте, что некоторые линии K находятся в плоскости yz и что эти линии вращаются вокруг оси Oz, что приводит к образованию определенной поверхности P, называемой плоскостью вращения. Начальная линия K называется начальным меридианом. Это меридианное уравнение F (y, z) = 0. (3) Возникает вопрос о том, что происходит с уравнением поверхности Р.
Для простоты предположим, что меридиан K лежит в этой части плоскости j / z (^ y ^ 0). Рассмотрим точку M (x, y, z) на поверхности P (подобно точке на поверхности P, точка M получается в результате процесса вращения из точки N начального меридиана K. В этом вращении , Точка N остается в плоскости и представляет собой окружность, которая перпендикулярна оси Oz и центр A которой находится на оси Oz, и ясно, что применение z точки N такое же, как применение точки M. В ординате радиус AN точно равен y4, но радиус AM аналогичен, тогда как последний радиус — это точки M (x, y, z) и A (0, 0, z). ) Это просто расстояние между, поэтому Рисунок 310
AM = Yx * + Y * — Вот так y * = Vx * + y *. (4) Поскольку точка N находится на меридиане / C, ее координаты удовлетворяют уравнению (3). так F (y \ z) = 0. Из этого и (4) *) = 0 (5) Если прямая не существует полностью в части y> 0 плоскости yz, она может оказаться y * <0. Тогда AN = —y * t откуда _ y * = -yv + y.
Получите уравнение вместо (5) Следовательно, координаты любой точки на поверхности P (x, y, r) во всех случаях удовлетворяют следующему уравнению: (6) Это желаемое уравнение для поверхности P. Вы можете видеть, что (6) можно получить, заменив ^ на zhУх1 из (3) — \ — у * <Рекомендуется запомнить эту ситуацию. Для вращения начального меридиана вокруг оси Oy уравнение для плоскости вращения является координатой z уравнения меридиана. Пример. Когда линия y = z вращается вокруг оси Oz, она образует коническую поверхность.
Согласно вышесказанному, это уравнение поверхности ztVx * — \ — y * = z или Оказывается, что коническая поверхность является квадричной поверхностью. Точно так же можно получить несколько квадратичных поверхностей, но во многих случаях выполняются другие преобразования, потому что были получены похожие поверхности.
№ 3. Поверхностное сжатие и растяжение. Сделайте P поверхность. Выберите положительное число k и замените каждую точку M ‘на поверхности P другой точкой M (x, y, r). (7) Другими словами, если вы увеличите расстояние всех точек P, k раз от плоскости ху. Если это так, уменьшите эти Расстояние в ~ раз (если k = ~, расстояние уменьшается в 3 раза).
В результате этой операции поверхность » преобразуется в новую поверхность про (Рисунок 311). Говорят, что это получается из P растяжением с коэффициентом k в направлении оси O (когда речь идет о сжатии; Zome, нервный! / я раз означает 3 раза сжатие). Чтобы найти уравнение для поверхности H, мы ставим вопрос о том, как узнать уравнение для начальной поверхности P. Уравнение P (8) Рисунок 311. F (x, y, z) = 0. Возьмите P в любой точке M (xty, z).
Взятые из точки M (x, y, f) на поверхности P, r и связаны связаны (7). Поскольку LG находится на P, координаты y, f) удовлетворяют уравнению (8). F (x, y, *) = 0. Заменить здесь равным значением / -> / -j- «поиск (9) Это уравнение, которое применяется ко всем точкам I, является уравнением I. Чтобы получить уравнение для вытянутой поверхности, измените z исходного уравнения поверхности Где k — модуль упругости при растяжении.
Пример. Пусть первой альфа-поверхностью будет плоскость z = 6t и коэффициент расширения A = 2. То есть удвоить заявку на все точки на плоскости. Согласно приведенному выше уравнению Удлиненная * поверхность будет у = 6. Другими словами, эта поверхность плоская.
Скорость r = 12. Конечно, этот факт геометрически очевиден, потому что это хороший пример вышеприведенного правила. Замечания. Правила записи поверхностных уравнений, полученных для данной поверхности растяжением в направлении оси Ox или оси Oy, также установлены. № 4. Эллипсоид. Подумайте об эллипсе ^ 4- ^ = 1
Лежа на самолете YZ. Когда этот эллипс принудительно вращается вокруг оси Oz, получается поверхность, называемая сфероидом. Согласно правилу, принятому в n ° 2, это эллипсоидальное уравнение xf, g9 B ■ (10) Протяните этот эллипсоид k раз в направлении оси Ox. В результате он достигает поверхности, также называемой эллипсоидом, с уравнением, полученным из (10) путем замены х на ~ о Для простоты пусть kb = a, тогда уравнение (11) имеет следующий вид: (12) б * т с «~ 1 # Это так называемое стандартное уравнение для эллипсоидов.
Числа a, b и c называются их полуосями. Из процесса получения эллипсоида ясно, что он имеет форму, показанную на рисунке. 312. В сечении эллипсоида (12) с произвольной плоскостью, параллельной одной из координат, легко понять, что получен эллипс. Например, z = 312 по эллипсу в плоскости. = Λ (-c <^ h <^ c), Рассмотрим все точки эллипсоида, где z = h. Но координаты JC и эти точки связаны соотношением a * • b * ‘c8-‘ Могу дать форму
Смотрите также:
| Плоскость | Преобразование координат |
| Прямая линия | Производные функции нескольких переменных |

