Оглавление:



Понятие о чистом сдвиге
- Концепция Netshift Условия. Из концепции тонна Рис 112D В некоторых случаях прочность и жесткость структурного элемента напрямую связаны с сопротивлением сдвигу материала. Поэтому
необходимо изучить текущую деформацию сдвига и соответствующее напряженно-деформированное состояние (см. §32). Как правило, оно всегда включает деформацию сдвига.
Для более детального изучения этой деформации была введена концепция чистого сдвига. При Людмила Фирмаль
чистом сдвиге прямоугольный элемент, выбранный вблизи точки и ориентированный определенным образом, испытывает только сдвиговую деформацию и не имеет бокового расширения. На указанную грань элемента действует только касательное
напряжение. 112) Таким образом, чистый сдвиг представляет собой вид плоского напряжения и состояния деформации, и он действует на два взаимно перпендикулярных участка, ориентированных в направлении только с касательным напряжением. Эти участки
- называются чистым сдвигом. Взяв эти места за оригинал, уравнения (3.3) и (3.4) Ah = AU = 0, tuh = -t в предыдущей главе, получим: AA = t sin2A; TA = -t cos? Однако. (4,1) (4.2) Уравнение (4.1) показывает, что a = 0 или все другие места исчезают только в местах чистого сдвига ^ и нормальное напряжение не равно нулю, как показано на рисунке.
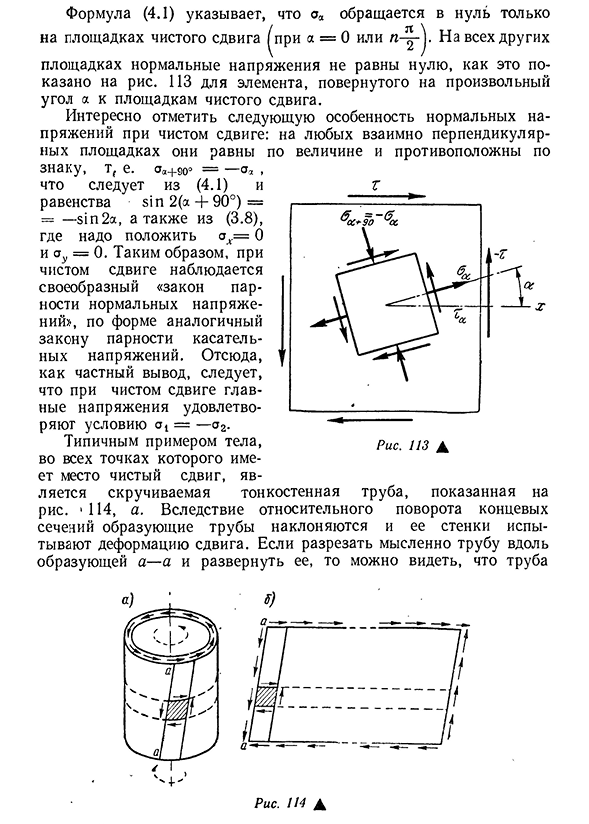
Поверните под любым углом А до 113 мест чистого сдвига для сдачи элементов. На взаимно перпендикулярных участках они равны по величине и противоположны по знаку, Tf E.STA + 9o ° = — (4.1) и уравнение sin2 (a + 90 °) == — sin2a, и (3.8 ) Из <ZX = 0 и AU = 0 чистого сдвига наблюдается «нормальный закон четности напряжений», который по форме похож на закон четности тангенциальных напряжений. Поэтому, как конкретный вывод, для чистых сдвигов главное напряжение является типичным примером тела во всех точках, где существуют чистые сдвиги — состояние O2-
Рис 113д Как показано на этом рисунке, витая тонкая труба. 1 114, а. Из-за Людмила Фирмаль
относительного вращения концов сформированная труба наклоняется, и ее стенки испытывают сдвиговую деформацию. Если вы порежете трубу вдоль мысленно сформированного а-а и расширите ее, вы обнаружите, что труба Опыт пластины, представляющей 121 чистый сдвиг. 114, б). Поскольку деформацию кручения практически невозможно создать в состоянии чистого напряжения сдвига, прикладывая тангенциальное напряжение непосредственно к краю пластины,
Смотрите также:
| Изменение объема материала при деформации | Анализ напряженного состояния при чистом сдвиге |
| Потенциальная энергия при объемном напряженном состоянии | Закон Гука при чистом сдвиге |

