Оглавление:







Деформированное состояние в точке
- Точка деформированного состояния 1. Основная деформация. Расширить в любом направлении Рассмотрим деформационные характеристики материала в плоском напряженном состоянии. Общий случай плоскости, когда бесконечно малый прямоугольный элемент со сторонами dx и dy произвольно ориентирован Его
109напряженного Фортуна действует на нормальное напряжение ау, ау и тангенциальное напряжение тул. — Дерево (рис. 106, а). Генерация этих напряжений сопровождается деформацией элемента. Позже мы сконцентрируемся на количественных отношениях между стрессом и напряжением, и сейчас обратим внимание только на их геометрические отношения. Учитывая деформацию элемента,
она происходит в плоскости вышеуказанного напряжения. Расширение Людмила Фирмаль
стороны элемента связано с действием нормального давления. Выразим их с помощью Adx и k.dy (рис. 106, б). Как уже упоминалось, сила линейной деформации в какой-то момент Рис 106А В § 5 он характеризуется значением удлинения в каждом направлении: е X & dx dx dx KDY ev = _ 1. ууууу «(3,34) Тангенциальное напряжение связано с угловой или сдвиговой деформацией. Это должно изменить исходный прямой угол на угол уха, называемый углом смещения, показанным на том же рисунке. 106, б. Представьте себе, что два
взаимно перпендикулярных сегмента длиной dx и dy проходят через интересующую точку в направлении осей x и y. В результате деформации эти сегменты подвергаются удлинению (3.34), что приводит к перпендикулярному изменению между ними относительно угла смещения CCS. Если вы теперь мысленно вращаете оси X и Y вокруг точки пересечения и последовательно комбинируете с различными сегментами, все положения оси будут все возможными для ее удлинения El, X и оси Y Набор удлинения и угла
- сдвига в зависимости от положения характеризует деформированное состояние в этой точке. Как установлено, любое плоское напряженное состояние уменьшается до двух взаимно перпендикулярных растяжений (сжатий) за счет основного напряжения и A2 (см. Пунктирную линию) Нона-Рис 106, а). Поскольку касательное напряжение равно нулю в точке основного напряжения, прямоугольные элементы, ориентированные в направлениях at и A2, растягиваются только, а угол сдвига равен нулю (на рис. 106). Исходя из этого, сегмент получает только расширения h и E2, и перпендикулярность между ними не изменяется, указывая на два
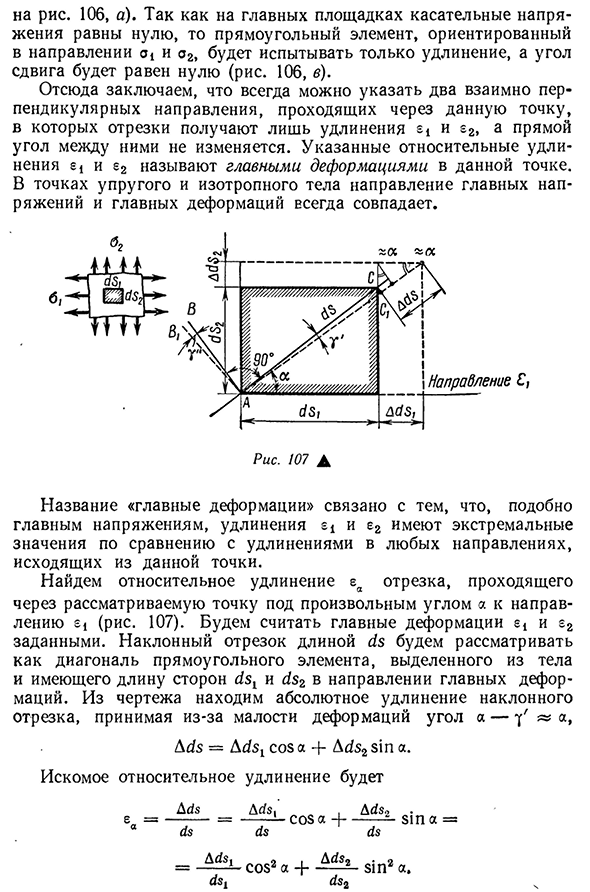
взаимно перпендикулярных направления, проходящих через данную точку. Это называется основной деформацией. С точки зрения упругости и изотропных тел направления главных напряжений и главных деформаций всегда совпадают. Название «главная деформация» связано с тем, что оно имеет экстремальные значения по сравнению с удлинением в любом направлении, исходящем из данной точки, таким как основное напряжение, удлинение и E2. Мы можем найти относительное удлинение EA отрезка, проходящего через рассматриваемую точку в любом направлении угла £ i (рис. 107). Рассмотрим основные деформации и E2.
Наклонный сегмент, имеющий длину ds, рассматривается как диагональная линия прямоугольного элемента, отделенного от основного корпуса, и Людмила Фирмаль
имеет длины сторон dsY и ds2 в основном направлении деформации. Из этого рисунка возьмите величину деформации для угла a-7 » a, Ads = Adsx cos a + Ads2sin a и найдите абсолютное удлинение наклонного сегмента. Желаемое удлинение Предполагая, что 111 = e и = E2, и используя тригонометрическую зависимость (3.5), чтобы окончательно получить EA = ecos2a-J-E2sin2a. (3.35), выражение (3.35) имеет вид Там) 2 2 Давайте посмотрим 31> Z2. Далее из уравнения (3.36) советник достигает максимального значения, когда cos2A = 1, то есть a = 0. В то же время Максимум е = е .. Но * И наоборот, при 2A
= 180 ° cos2a = -1 советник достигает минимального значения: Минимум е = Е2 «. Если величина и направление основной деформации в точке известны, удлинение в любом направлении определяется уравнением (3.35) или (3.36). Чтобы сделать выражение деформации материала в этой точке более ясным, мы узнаем, как оно поднимается. Обрежьте точку в вопросе 108, чтобы сформировать материальный элемент в виде небольшого круга с радиусом dr).
Формула для кругового контура перед преобразованием принимает вид (США. dx2 + dy2 = dr2. Ось X и ось Y расположены в основном направлении деформации. После преобразования координаты точки контура следующие. dxr = dx + & dx = (1 + e) dx; dyx = dy + -kdy = (1 + e2) dy. (6) Из 112поставляя (б) (а) значения dx и dy, получаем dx ** Y2_j K1 + e jd r] 2 + ((1 + e2) dr] 2 Это уравнение является эллиптическим уравнением с полуосью, равной (1 4-e ^ g и (1 4-e2) dr вдоль основной деформации. Следовательно, состояние деформации плоскости в этой точке состоит в том, что бесконечно малый круговой элемент
материала, выбранный в окрестности этой точки, не совпадает с основным направлением EP с основными деформациями b = линиями AB и AC, перпендикулярными друг другу108 Получает ea и EA + 90o, прямой угол между ними изменяется в зависимости от значения угла сдвига. 2. Аналогия уравнения напряжения и деформации в определенный момент времени Найти угол сдвига между двумя взаимно перпендикулярными отрезками AC и AB, расположенными под углом a в направлении основной деформации (см. Рис. 107). Сегмент AC в результате деформации повернут на угол y ‘, который можно определить как отношение дуги CCi и радиуса AC = ds, , _CXX_Ads, Sin Ads2cosa ds ds ds ‘ или , & ds,. Реклама, «■ y = ——- Sin cos a
———- I-cos sin a = дс, ■ дс2 -S с 2А. ) два Чтобы определить Y «- угол поворота прямой AB — угол a в формуле (b) следует заменить на (a | / -90o). Тогда мы получим y» -. … £] — £ 2. s in2 (a-j-90 °) = —— ~ 1L2_Sin 2a. (г) 2 2 Различные символы (b) и (d) в уравнении указывают, что сегменты AC и AB вращаются из своих недеформированных положений в разных направлениях, как показано на рисунке. 107 Требуемый угол смещения, равный вашему изменению под прямым углом, равен сумме значений b ‘c o l y t n s x y’ и 7 «. 7a = (ex-e2) s in2a. (3.37.) 113 формулы (3.36) и (3.37) пишут вместе в следующем формате
е1 4-е2 два e1-e2 4-cos2a; два восемь » 7а два (3,38) —— Грех 2А. два Напомним уравнения (3.14) и (3.15), которые представляют условия плоского напряжения в точке A_CTi + g2_j_? я-g2coS2a; а2 2 (D) т грех 2а. «2» Зависимости (3.38) и (е) показывают математическую идентичность закона распределения напряжений а, а 4-та — е я, 2 — , ТА и преобразование баллов. На основе указанного идентификатора выходных данных написать, например, выражение «» — ^ + 4 (т Н • (3’39) Это записывается по аналогии с (3.13), где Ah, AU, Tux заменяются соответствующим искажением GC, EU, Tux-выражением (3.39). Это из (3.39) ex4-E2 == ex4-EU = const, то есть сумма относительных расширений в направлении, перпендикулярном друг другу в данной точке, является постоянной величиной. Аналогичная
позиция представлена уравнением напряженного состояния (3.8). Отметим также, что эта аналогия позволяет графически представить деформацию в точке, используя круг молей. В заключение можно сказать, что здесь рассматриваются только деформации, возникающие в плоскости основного напряжения. Распространенным случаем деформации материала в точках является объемный характер. В этом случае математическая аналогия, полученная из плоской задачи в распределении напряжений и напряжений, сохраняется в задаче объема. Таким образом, в общем, в каждой точке тела вы можете указать три основных деформации: e, E2 и E3. Если бесконечно малый сферический элемент обрезается вокруг точки, элемент растягивается в направлении a = EP в точке упругого изотропного тела, как это было сделано с плоской задачей.
Смотрите также:
| Понятие о траекториях главных напряжений | Закон Гука при плоском и объемном напряженных состояниях |
| Объемное напряженное состояние | Изменение объема материала при деформации |

