Оглавление:







Особенности работы трехфазных систем, вызываемые гармониками, кратными 3
Характеристики работы трехфазной системы, вызванные гармониками, кратными 3. Электродвижущая сила в каждой фазе трехфазного трансформатора или трехфазного генератора часто является несинусоидальной.
- Каждую ЭДС (есть, ev, ес) можно разложить на гармоники, повторяя оставшиеся формы со сдвигом 1/3 периода j. Обычно нет постоянных компонентов.
Фаза A, где k — гармоника эдс, равна. Людмила Фирмаль
Что касается эдс, фаза B задерживается от эдс-фазы А-So, а эдс эдс фазы C «1 секунда» опережает эдс-фазы фазы А и фазы C, и гармоники k k равны соответственно , = Ekm sin (.kat-120% -fC> L); I * ekc = Ekm sin = Ekm sin (ku> t 4-120% 4-a |> *); ku k- = k— = 120% ,
Если sz sk принимает значения 1.4, 7.10, k является гармоникой эдс B, фаза находится на 120 ° позади k гармоники эдс A. В результате гармоники 1, 4, 7, 10 находятся в прямой последовательности фаз Формируйте систему (понимаемую прямым фазовым секвенированием, см. §154) Для k = 2, 5, 8 и 11, Л — гармоника эдс, фаза B на 120 ° опережает гармонику фазы A k. В результате вторая, пятая, восьмая и т. Д.
- Гармоники образуют систему обратной последовательности. Гармоники, кратные 3 (k = 3, 6, 9, …), образуют систему нулевой последовательности. То есть третья гармоника всех трех фаз находится в фазе (3-120 ° = 360 °): e3d = eV-ecz ~ ezt s ^ n (3C0 / 4 «^ 3)» шестая гармоника Также фаза соответствует.
Тот факт, что третьи гармоники всех трех фаз находятся в фазе, помогает наглядно показать это. 221 эдс эд, эв, ес — 3-х фазная эдс трехфазного генератора. Они имеют прямоугольную форму и смещены друг от друга на треть периода основной частоты. На рисунке показана первая и третья гармоники каждой эдс, но на рисунке показано, что
третья гармоника фактически находится в фазе. Людмила Фирмаль
Описывает характеристики трехфазной системы, вызванной гармониками, кратными 3. Если обмотки трехфазного генератора или трехфазного трансформатора треугольные (рис. 222, а), гармоники, кратные 3, будут течь, даже если нет внешней нагрузки.
Алгебраический суммирующий треугольник третьей гармоники эдс равен ЗЕ3 *. Когда сопротивление обмотки каждой фазы третьей гармоники выражается Zs, ток третьей гармоники треугольника выглядит следующим образом. Рис. 221, где E9 — эффективное значение шестой гармоники фазовой эдс, а Zo — фазовое сопротивление шестой гармоники.
Среднеквадратичное значение 222, а тока, протекающего по замкнутому треугольнику цепи на рисунке, равно: / =] / -f- + I * + •• 2. Обмотка трехфазного генератора или трехфазного трансформатора
Если провод подключен к белому треугольнику (рис. 222, б), если в нем присутствует фазовая эдс, гармоника, кратная s 3, то клеммы t и n имеют напряжение, равное сумме эдс, кратной 3 Гармоника Chn = SE3m sin (3coZ + φ3) -j-ЗЕ9msin (bso / + Фе) + … П
оказание вольтметра схемы 222, b равно: U ^ 3] ^ El + El + … • Однако алгебраическая сумма первой гармоники e. д.с. и все гармоники е. Значение d.s. равно нулю, поскольку оно не кратно 3.
Следовательно, ток не течет через замкнутый треугольник из гармоник, перечисленных при отсутствии нагрузки. 3. При линейном напряжении гармоника из трех кратных отсутствует, независимо от того, соединены ли обмотки генератора или трансформатора звездой или треугольником.
Продемонстрировать третью характеристику в случае холостого хода генератора или трансформатора, то есть без внешней нагрузки. Однако это свойство также применяется при загрузке. Сначала рассмотрим схему треугольного соединения (рис. 222, а). <pd3 — указывает потенциал в точке A и (pBz — потенциал в точке B 3-й гармоники, FLZ = <GV.Z ^ 3 “WL But / 323, следовательно, R.
Рис. 221 при подключении к звезде ( Рисунок 223) Третья гармоника линейного напряжения равна разности, соответствующей фазному напряжению, потому что третья гармоника фазного напряжения находится в фазе и вычитается при построении этой разности. (Обычно постоянная составляющая отсутствует) / ^ + ^ + ^ + C2 + Inline
Рис. 223 Напряжение цепи не имеет гармоник, кратных 3, поэтому il = V 3 / и * + < + <T + .. • <V3, если существуют гармоники, кратные износу-3, Vph 4.
Если звезда имеет равномерную нагрузку и не имеет нейтральной линии, третья гармоника нулевой последовательности и другие гармоники Волновой ток не может течь по линейному проводу (это было подробно объяснено в §152) 224 при Zo = oo) Напряжение ioo ~ ^ 3m s * n 3U / — | -φ3) j- /; в / SIN SIN (6U / φ6) — | — будет действовать …
Его фактическое значение 5. В схеме звезда-звезда с равномерной фазовой нагрузкой, когда сопротивление нагрузки третьей гармоники представлено Zw3, а сопротивление нейтрали третьей гармоники представлено Zr3 (рисунок 224), ток третьей гармоники
Протекает к нулевой линии. Точно так же ток от других гармоник кратен трем. Пример 97. Мгновенное значение напряжения фазы А трехфазного генератора выглядит следующим образом. АА = 127 sin (10/10) + 30 sin (3 / + 20 ‘) + 4-20 sin (11 27 UTsin ((>) / + 40 °) 4− 20 / З «грех (11ш / -15 °) в.
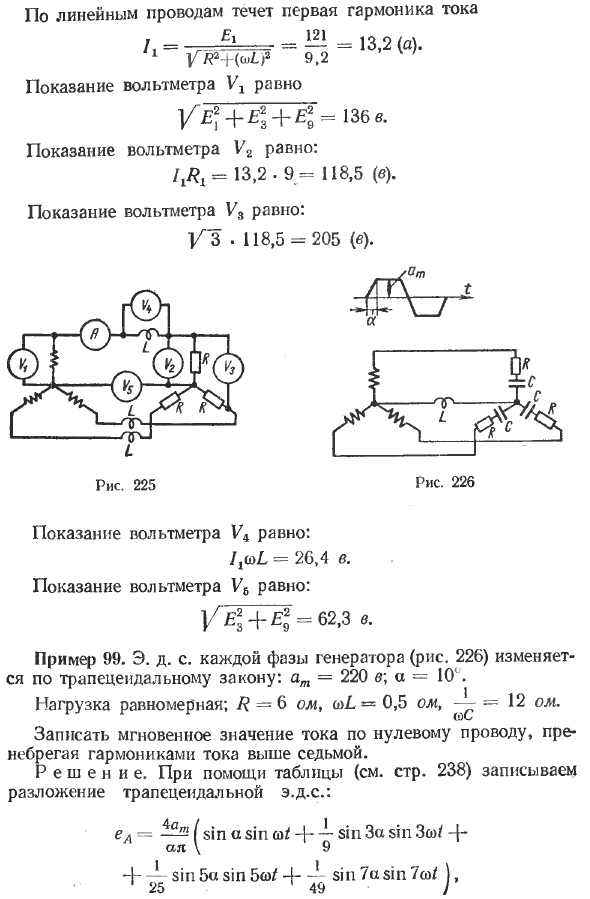
Пример 98. Фаза A 225 цепи на диаграмме ЭДС эквивалентна: еА-170 sinω / — | -4-80 cosЗю / + 34 cos9ю / в; = 9olg, ω £ = 2ol Определяет все показания прибора. Устройство электродинамической системы.
Решения. Допустимые значения эдс: E, = — ^ = 121 (c); £ 3 = 56,5 В; £ в = 24,2 дюйма V 2 Первая гармоника тока протекает по линейному проводу 71 = «9 ^» 13,2 напряжения Общее чтение V \ равно / £ * 4- £ 23 + ^ = 13BV. Измеренное значение вольтметра V2 равно следующему значению. / ^ = 13,2,9 = 118,5 (с).
Показания вольтметра V3: / 3. 118,5 = 205 (с). Показания вольтметра V4 следующие: l ^ toL = 26,4 дюйма V6 вольтметр показания следующие: 1 / £ H £ 9 = 62-3 в примере 99. Е. д. Фаза генератора (рис. 226) изменяется по трапециевидному закону: am = 220 В \ a = 10 ‘. Нагрузка равномерная. R = 6 кОм (дл = 0,5 кОм, — ^ = 12 кОм (° C).
Игнорировать гармоники токов больше 7-го и записывать мгновенные значения тока вдоль нулевого провода. (См. Стр. 238). Опишите разложение трапециевидной электродвижущей силы: или 4. 220 (грех 10 грех 4-грех 30r грех Зю / 4 ~ at = ~ -7t 18 * I 4 * -J- грех 50 ° sin 5co / 4— sin 70 ‘sin 7cd / ^. 25’ 49)
Следовательно, есть = 274 sin <1/4 до 89,3 sinZSO / 4 «49,5 sin 5 (0/4» 30,9 sin 7 <ат. 3 тока Через нулевой провод протекает только вторая гармоника: = 31,8e_ / 0 a. 7СЗ1,5 / + 2- / 1,33 мгновенное значение тока / 03 = 44,8 sin (ЗСО / -4 ’40’) a.
Смотрите также:
| Активная и полная мощности несинусоидального тока. | Биения. |
| Замена несинусоидальных токов и напряжений эквивалентными синусоидальными. | Модулированные колебания. |

