Оглавление:


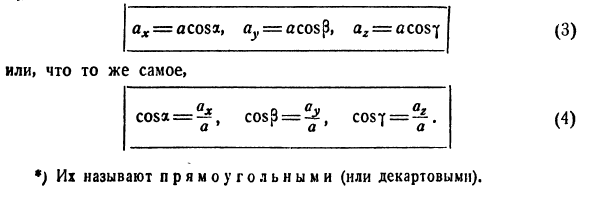

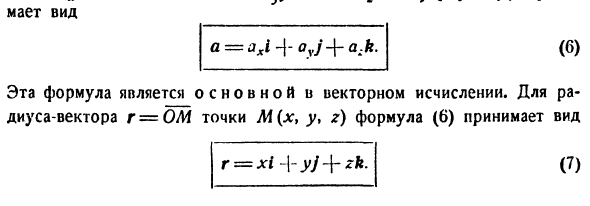




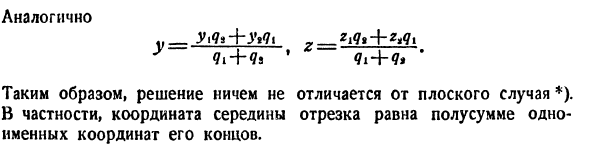

Координаты в пространстве
- Пространственные координаты № 1. Определение и обозначение. Пройдите через точку O (начало координат) в пространстве и пройдите через три взаимно перпендикулярных координатных оси Ox, Oy, Oz (рис. 278). Поворот на 90 ° вроде бы происходит Как хорошо + * Qi + q * ‘ Таким образом, решение такое же, как в плоском корпусе *). В частности, центральная координата сегмента равна половине суммы одноименных координат на его концах.
Counterclockwise. Единичные векторы для осей Ox, Oy и Oz представлены I, j и k соответственно. Любая точка M в пространстве имеет определенные координаты на каждой указанной оси. Эти координаты называются *) #: x-абсцисса, y-ордината, z-репликация. Тот факт, что координаты M равны x, y, z, описывается следующим образом: М (х, у, z). Вектор OM = r от начала координат до точки M называется радиальным сектором этой точки. Поскольку начало координат O имеет координаты (0, 0, 0) и проекция вектора на ось координат равна конечной координате без исходной координаты, PrxOM = x-0, Или Upxr = х.
То же самое относится и к другим осям. так 0) Рисунок 278. x = Prx, y = PrG, r = Prg. Координаты точек — это проекции радиального отражателя на соответствующие оси координат. Это также записывается в виде a {ах, ау, я}. Также помните, что длина вектора а обозначена буквой а. Если координаты точек N и K равны (xN, yN, zN) и (xk, yk, zK) соответственно из n ° 2 в § 2 согласно теореме 2 (2) \ x = xK-xN, ay = yK-yN, az = zK-zN Когда угол вектора a и осей Oxt Oy и Oz равны * »P» T> (теорема 5 n ° 2§2)
Проекция любого вектора a = NK на оси Ox, Oy, Oz представлена ax, ay, az. Людмила Фирмаль
ax = acosd, aU = acosp, az = acos] f наиболее распространенным axa cosa = -, a * COSp = 2 * a • ° r cosi = -j. Они называются прямоугольниками (или декартовыми).Числа cosa, cosp и cosy называются направляющие косинусы вектора а. № 2. Основная формула для векторного расчета. Длина вектора Соотношение между направляющими косинусами. Расстояние между двумя точками. Уравнение поверхности шара. Докажем следующую важную теорему. Теорема. Все векторы являются суммой компонент по осям Oh, Oy, Oz. Доказательство.
При переводе вектора его компоненты не меняются, а просто скользят по соответствующей оси. Следовательно, мм, целевой вектор a может быть перемещен. Следовательно, его начало N совпадает с началом координат O. Все три компонента имеют общее происхождение для О. 279 понятно Рисунок 279. 3 года OK = a, AN = OB, IR = OS. так (5) a = OA — \ — OB + OS, но Это доказывает теорему, потому что OA, OB и OS являются компонентами вектора a точно вдоль координатной оси. Напомним, что алгебраическое значение компонента OA вектора a вдоль оси Ox является только проекцией вектора a оси a на ось Ox.
Водоросли привели. (ОА) = Ах. (Теорема 1 n ° 6§1), движущийся вектор равен его алгебраическому значению, умноженному на вектор его базовой единицы, OA = aL. Аналогичным образом принимаются ОВ = a J, OC = a, k и уравнение (5).a = axi aj + a.k. (7) Смотри Эта формула является основой для векторных расчетов. Если радиус-вектор r = OM точки M (x, y, z), уравнение (6) принимает вид r = xi + yj + zk.
- Возвращаясь к рисунку 279. Это указывает на то, что вектор OK является гипотенузой прямоугольного треугольника PMC. Следовательно, по теореме Пифагора Квадратичное применение теоремы Пифагора (к треугольнику OAI) w | 9 = | OL | 9 + \ U \ Откуда | ok | * = | OL | «-IL7 / | * 4- Но потому что ~ AN == OB, U = OS, Отметим, что длина компонент OA, OB, OS вектора a = OK отличается только по знаку от проекций ah, ay, aq. (9) Мы получаем a * = a’x + a * + a} и a = V a \ + a} + a То есть длина вектора равна квадратному корню из суммы квадратов проекций на осях.
Объединение уравнений (4) и (9) показывает, как узнать проекцию вектора и найти его косинус направления. Замена уравнения (3) на ah, ay, aq в (8) и уменьшение результата на π9 дает следующее соотношение: (10) cos9 a — {- cos9 p -J- cos9 7 = 1 «То есть сумма квадратов направляющих косинусов любого вектора равна 1. Задача нахождения расстояния d между двумя точками N (xn> Yk * ^ n-) с использованием уравнения (9) решается непосредственно K (Xk, yk, zK). Фактически это расстояние — длина вектора проекции НК на ось, равная xz — xNt y k — y,% 2k-Zfl. (II), d = y (xk-lgdg) * + (yk-y »? + (zk-zs) \
В заключение рассмотрим поверхность шара с центром C (a, b, c) и радиусом R. Точка CM (x, y, z) находится на этой поверхности, только если \ CM \ = R. время (Х-с) * Сай-б? + (Z-c? = R \ Таким образом, уравнение (12) является рассматриваемым уравнением поверхности. (13) № 3. Сегментная классификация для этого. Предположим, что заданы точки Mi (xv ylt zx) и yi, z%) и число q > 0. Точка M (x, y, z), которая делит MtM9 на отрезок (12) M1M_q ± LS, ~ qt
Если центр шара находится в начале координат, уравнение имеет более простой вид Людмила Фирмаль
По этой причине обратите внимание, что вектор UI | Л1 и MMt параллельны и направлены в одном направлении. Однако вектор MtM взят из MM) <71 умножение MiM = -MM * I * Когда это уравнение *) проецируется на ось Ox, в Отсюда •) Проекция равных векторов одинакова (на одну и ту же ось). Так из равенства а = б (4) Если делать ох = шх <*) Переход от соотношения () к (* ♦) называется проекцией уравнения на ось Ox («) \
Смотрите также:
| Векторы | Скалярное произведение векторов |
| Проекции | Векторное произведение |

