Оглавление:






Определители 2-го порядка
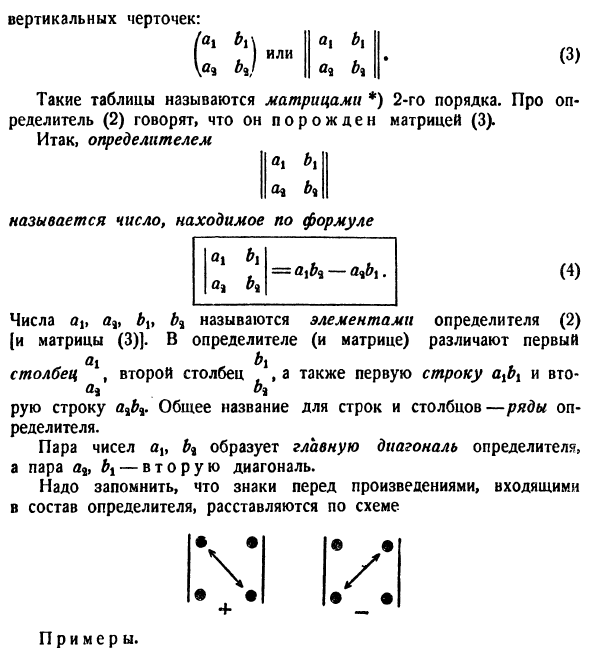
- Вторичные детерминанты ps1. Определение. Многие математические вопросы используют специальные выражения, называемые определителями (или определителями). Простейшим из них является так называемый квадратичный определитель. «Я показываю, как эти детерминанты возникают при решении двух линейных уравнений с двумя неизвестными. Просмотрите систему aix + biy = ru afx + b% y = r <i. Чтобы исключить неизвестный y, умножьте второе уравнение на bt и вычтите результат из первого уравнения. (A \ bf-a% b ) x = T \ b <i-mph . Коэффициент х записывается как О бх (2) Во времени Это называется квадратичным определителем.
Его местоположение задается квадратным столом Я, б Окруженные скобками или двумя ларами, чтобы подчеркнуть, что эта таблица считается в целом Вертикальная линия: h oi bx или V »» BJ B * Такая таблица называется квадратичной матрицей *). Определитель (2) называется порожденным матрицей (3).
Следовательно, квадратичный определитель — это конкретное число, определяемое как числа a b b, b so и их относительные положения. Людмила Фирмаль
Итак, детерминанты A, BX BC Называется число, найденное в формуле Числа a it a9, b3 называются элементами определителя (2) [и матрицы (3)]. Определитель (и матрица), первый (4) Столбец, второй столбец, первый ряд ajbi и второй Abi Общее имя для строк и столбцов — это ранг определителя. Пара чисел a19 образует главную диагональ определителя, а пары g2 и bx образуют вторую диагональ. Следует помнить, что символы перед кусочками, составляющими определитель, расположены по схеме •• e » л / • + •••
Пример.4 1 5 2 6 7 4 = 35- 12 = 23, -26, -2 6 = 14 1 7 O 4 2 sin x-cos x cos x sin * 24 + 2 = 26 3 5, „3 5 ) Читатели должны четко понимать различия в детерминантах с, <* я би И матрица af bs ag bt Таблица, состоящая из четырех чисел. Первое число, второе просто № 2. Шесть основных свойств квадратичного определителя. I. Если строка используется в качестве столбца, а столбец используется для строки, определитель не изменяется. Baiagu a * bi bx b * Фактически, каждый записанный определитель равен afii-af ^, поэтому они равны друг другу. Это свойство определителя означает, что строки и столбцы в точности равны.
- Поэтому для простоты создайте дополнительные свойства только для строк. II. Определитель меняет знак при перестановке строк: Bx b * A * H BX Фактически, левая сторона здесь — это axb% -ajbx, а правая — (aA-i ^). Это то же самое III. Если строки определителя совпадают, определитель равен нулю: а б А = 0. а б На самом деле *) записанный определитель ab-i £ = 0. Внутривенно Когда все элементы в любой строке определителя умножаются на определенное число q, весь определитель умножается на это число. а я бх-о би % b% -h (к бг
Фактически обе стороны равны q (axb j). V. Если элемент в одной строке пропорционален элементу в другой строке, определитель равен нулю. Хаа1 ба \ ♦) По следующим причинам: из-за перемещения строк определитель меняет знак, но если строки совпадают, их перестановки не изменяют определитель. Если определитель представлен x, то x = -x и η = 0.
Проверенные свойства также позволяют следующую формулировку: Общие факторы для линейных элементов могут быть взяты из символа решения. Людмила Фирмаль
Эго следует сразу за характеристиками III и IV, и записанные детерминанты qafix-q <* \ bx = 0. VI. Если какой-либо из s / procs умножается на другое число и умножается на любое число, определитель не изменяется. Например, добавьте вторую строку, умноженную на q, к первой строке. Это приводит к детерминантам <* \ + qa% bx — \ — qb% а * б ах бх а9 чч равных (I, + qa%) bg-a% (b {+ qbt) = a {b% -afx Это свойство является наиболее важным из всех шести, как описано ниже.
Смотрите также:
| Механические применения определенного интеграла | Определители 3-го порядка |
| Приближенное вычисление определенных интегралов | Определители любого порядка |

