Оглавление:






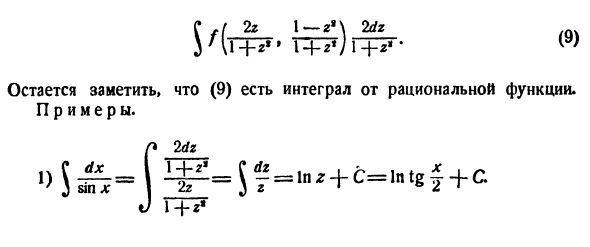


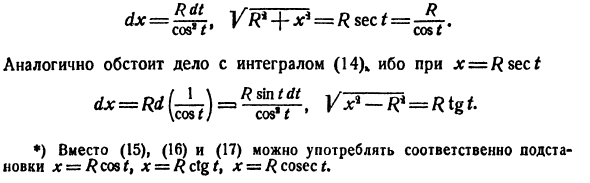

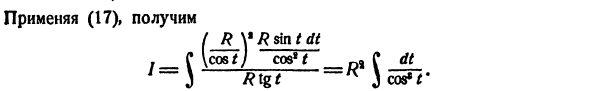




Интегрирование некоторых трансцендентных функций
Интеграция нескольких трансцендентных функций n ° 1. Интеграция J e ° * P (x) dx, \ P (q) sinax dx, JP (x) cos ax dx. Для указанного интегрирования, если P (x) означает целочисленный полином от AxnBxl до x- \ -…- \ -Kx — \ — L, интеграл вычисляется путем интегрирования с компонентами. Конечно, позвольте мне объяснить хотя бы первый из этих интегралов.
- То есть, когда η = 1, интеграл равен -Incosx + C. Для 1 интеграл конвертируется следующим образом: = \ tg «» * xd (tg X) -5 tg «-» X dx. Первый интеграл справа вычисляется напрямую, а второй имеет ту же форму, что и (6), но проще, поскольку порядок tg jc уменьшается на 2 единицы. Цель достигается путем многократного применения этой техники.
Где n — натуральное число, полученное с использованием того же метода декомпрессии, который описан в предыдущем n °. Людмила Фирмаль
Точно так же, \ ztgnxdx, Для ctg1 x dx = -1) dx = -d (ct g x) -dx пример. 1) / = * Jig’xdx = Jtg * x 1) dx = X ££ -5tg * xdx. Отсюда № 5 • Интегрирование разумных функций для In * и cos x * Интеграл, рассмотренный в n ° 3 и 4, является частным случаем интегрирования. Дж / (грех х, соз х) дх, (7) / (», V) — рациональная функция аргумента.
Как мы видели, в этих конкретных случаях есть удобные методы расчета, которые специально адаптированы для них. Но есть Универсальная перестановка, которая позволяет любому интегралу (7) привести к интегралу рациональной функции. Это замена (8) На самом деле, в этом случае jc = 2arctg z, Откуда , 2 дз дх = т +? — с другой стороны, , х грех 2 ~ * l: C03T 2tgT sin x — 2 sin y cos y = 2 —j— = — l + tg’Y потому что> у Грех «^ 1 — потому что «4 л-тг» £ A A A A Z I COS X— COS -s-— Sin * TP = 2 2 1 _,. F, * ‘ 1 + tg’y > * Cos -k- так 2z 1-2 » И в результате подстановки (8) интеграл (7) преобразуется в следующую форму:
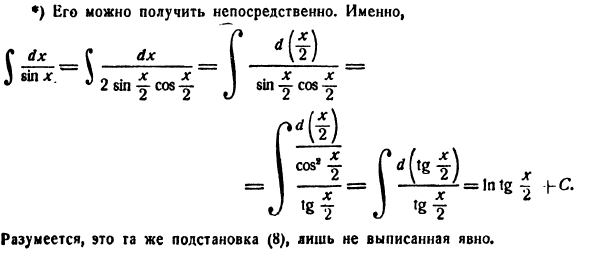
Отметим, что (9) является рациональным интегралом функций. Пример. C 2 (11 J 1 + Z- равенство дх Cos x = 5 / Это удобно помнить *). 2) Интегральный Его также можно рассчитать с помощью подстановки (8). Однако проще переписать 1 как NL J грех (10) дать немедленно в связи с дх cos * x 4 «b% sin * x * (А) ‘= | х! е (м + м) + с В некоторых случаях подстановка <gjr = z полезна. Например, тогда дх (Тг х) ft8 I C cos * x _ C d (tgx) 1 f d (\ zx) А (на основании таблицы формулы XI)
- •) Можно получить напрямую. просто Конечно, это та же перестановка (8), но она явно не описана.Тип (11) интеграл уменьшает интеграл ghrt («> *>» » Например, / -C ** ~) До 5 + 3 cos * ‘ дх р дх -s 5 sin’sin’J + 4cos »y + sin, y J 4 + tgfy № 6. Тригонометрическая замена. Пусть f (u, y) — рациональная функция аргумента. Тогда каждый интеграл $ / (*> VR * -x *) dxt (12) \ f (x, VWT ^) dxt (13) \ f {xt Vx% -R *) dx (14)
*. Эти замены следующие: *): Интеграция (12) х = /? sinf, (15) (13) x = Rtgt (16) И (14) х = Rsect. (17) На самом деле, если jc = R sin f dx = R cos / dt, VRi-xi = R cos t s
Сводится к интегралу рациональной функции по sin t и cos t с использованием соответствующей тригонометрической подстановки функции Людмила Фирмаль
Если x = Rsect, ситуация аналогична интеграции (14)>. *) Вместо (15), (16) и (17) можно использовать перестановки x = Rcost, x = Rctgt, x = Rcosect соответственно.Давайте посмотрим на некоторые примеры. Используя (15), 1) / = $ Y R * -хЧх = \ (R cos t) (R cos t) dt = = R% ^ cos ^ (1 + cos 2 /) dt Отсюда -f ^ sin 2/4-C = ^ arcsin ~ + Y sin * cos * -fC Наконец *) / arcsin A + g Очки C ^ f Rcostdt_ if if / 1. #, R Отсюда j_ 1 /? sln <. r_J ^ x | .p дх 3) / = 5 Теперь примените замену (16): ОДТ cos11_ iСcos t dt___1_ 1, t% t R ~ R *) R * ‘skit * л cos / но Раздел R s € C t ■ Так _ / _ VE + Za-T
Применить (17) и получить (I9 D 8in t dt \ adv, 1 cos 4 /? тг т предположение P (x) = u, du = F (x) dx, eaxdx = dv, v = -eax, Вы найдете ^ eaxP (x) dx = eax- ~ ^ eaxPr (x) dx. Правый интеграл относится к тому же типу, что и левый интеграл, но коэффициент P ‘(x) имеет степень, меньшую P (x). Цель достигается путем многократного применения этой техники. Расчеты аналогичны для других интегралов, показанных в заголовке. Пример. 1) -bx — \ — $) e * dx.
При интеграции в части, / = (Jc * -bx + 6) e * — \ (2x-5) e * dx (1) Путем вторичной интеграции деталей, J (2x-5) e * dx = (2x-5) ec-J 2ex dx = (2x-7) e + C. Подставляя это в (1) / = (Π * -7x +)) ex + C 2) 1 = \ (12×1-6x) sin 2xdx. предположение 12x * -6x = и du = (24x-6) dx, sin 2xdx = dvt v = — Мы получаем / = (Ev: -6x *) cos 2x -} — \ (12x-3) cos 2x dx.
Последний интеграл проще всего вычислить следующим образом: Si.e .— Разбивает целую дробь на простые дроби. 1 _ A, B C, D (G-1) «(* + 1)» — (* — I) — * — I ‘(g + ) * » Отсюда Если z = 1, то r = -1, тогда A = C = ~. Сравнение коэффициентов для r * и r® = 1 B + D = 0, A — D + откуда D = 5 = —так (Поскольку r = sinjc <1, а положительное число должно быть ниже логарифма, вы должны написать In (1 — z)> вместо In (z — 1)). Вот так 4 [I-sin t • I-sin * t J • 4 [1-surt ‘cos * t J’ *
Конечно, прежде чем применять рекомендованную «замену» к тому или иному интегралу, необходимо проверить, можно ли его вычислить. •) Читать дальше: / = y [In (sec + tg t) + см. C \ gt \ + C Ho R * sect \ gt = xY xl-R *. Кроме того, поскольку R является константой, In (sec t + Ig t) ss In (R sec t + R tgt) -In R = In (a + K * -R *) + Cv
Интеграция проще. Например, интеграл l = \ xV ** + R * Применение dx-подстановки нелепо (16) + + Ka) = | (** + R ‘) 1 «+ C. В заключение отметим, что подстановка (16) также успешно применяется к некоторым интегралам рациональных чисел. Например, интеграл дх PT В знаменателе есть дроби с несколькими мнимыми корнями. Поэтому здесь мы имеем дело именно с случаями, которые не рассматривались в §2. Предполагая, что x = tgt: ‘= $ S J 0’ + cos 2 <> «-T + PG + C так ._arctg x. sin / cos t, n_arctgjc, tglcos ‘t, r I-2 I 2 I 2 I 2 Наконец / ^ (Arctgx + ^ + C перераспределение 12L: -3 cos 2x dx узнать (\ 2x — 3) cos 2xdx = Остальное понятно.
du = \ 2dx, грех 2x Vz == 2 * -y) грех 2x —6 я грешу 2lg </ x. n ° 2. Интеграл J P (x) 1 день x dx. Если письменный интеграл P (jc) является целочисленным полиномом и n является натуральным числом, дх «X = u, du-n lnn_, jc-, х к P (x) dx = dv, v = Q (x),> r Здесь Q (x) может означать обратную производную от P (x) без свободных членов. ^^ — это многочлен того же порядка, что и P (x). Следовательно, формула ^ P (x) ln «xdx = Q (x) lnax-n ^ Qj ^ ln ^ xdx Уменьшите исходное интегральное вычисление до более простого аналогичного вида.
Пример. Дай мне / == 5 (32 ^ -9 ^ + 12jc-f- Олн ^ jc ^ / jc. верить * * *: = U, du = 2 \ nx ^ t F (32. * 8-9dg + 12x + 1) dx = dv, v = 8x * -3x * + 6 jt’-fx. тогда / = (8xi-Zdr8-f 6dg + x) In * dg-2 \ (8 * 3-3jc * + 6x + 1) In x dx. Интеграция снова для каждой части. 1px = u, du—, (8 x3-3jc «+ bx -f 1) dx = dv, v = 2x * -x3 -f 3 ** -f-x. тогда 5 (8jc * — & * ■ + «* + l) lnx <te = s = (2x * -x * + 3x * + x) \ nx-J (2n3-x * + bx + 1) dx. В остальном все понятно. n ° 3. Интеграция J sin «x cosm x dx. Письменный интеграл (где n и m — неотрицательные целые числа) разлагается на две формы. а) хотя бы одно из чисел n или m является нечетным числом б) Оба эти числа являются четными числами. Если а), интеграл J shr * co $ mxdx (2)
INTEGRALSJ.Inш »shGm4kh Естественно, он рассчитывается методом, называемым открытым методом расщепления. Суть видно из примеров. / = J sin w x cos8xdx. Из коэффициента cos3 * (нечетная сила!). Разделите один коэффициент cos x * и используйте тот факт, что cos xdx = d ($ mx). Это большой-да l = \ sin 94 x cos9 xd (sin x). Ho cos * x = 1-sin * x.
Так что если вы используете подстановку sin x = z (что имеет в виду) / = jj sinwjc (l-sin “jc) rf (sin = аналогично / = J sin8xcos®xdx = −J sin4l: cos®xrf (cos x). Отсюда / = -J (1-cos ‘x) * cos8 xd (cos x) = _ _COS7 X | 2 cos * x cos «Xr -7 ‘9 11 «Я» c- Если оба показателя pit нечетные, расщепление * лучше всего делать из коэффициентов расщепления с помощью sinp x, coswjc, меньший индекс *). Например, интеграл l = \ sin3 x cos47 x dx Он должен быть рассчитан следующим образом: г C / O около 47 Дж / ч cos60JC COS48 *. — / = — \ (1-cos4 x) cos xd (cos- ^ ——— C.
Перепишите интеграл в виде / = $ sin5 * (l-sinsin x), Далее нам нужно расширить (1-sin **) 93 до степени греха x, что, конечно, очень громоздко. В примере (а) интеграция (2) рассматривалась только в качестве примера, но ясно, что вышеуказанный метод имеет общие характеристики. 6,,. _ / sin 2dg \ i *) Если η = π, установите sin ** cos ** на (- ^ — I.
Чтобы вычислить интеграл (2) в случае б), необходимо применить переход к двойному углу. То есть используйте известную тригонометрическую формулу. _ _ Sin 2a / f4v sin a cos a = —y, (3) , • 1 — cos2a грех, а = -5-, (4) , 1 + COS 2A cos9 a = -1-2-. (5) Обратите внимание, что вы можете ограничиться уравнениями (4) и (5). Однако это необходимо делать всякий раз, когда уравнение (3) имеет значение. Пример. 1) sin’jc coskxdx.
В переписать / формат / = J (sin x cos x)% cos1 x dx Примените уравнения (3) и (b). \ s * n9 2l; (1 -j-cos 2x) dx = = — ^ sin% 2xdx + ^ sin12xco $ 2xdx. Конец письменного интеграла принадлежит типу а), формула (4y. / = -L ^ (1-cos 4l 🙂 dx + ^ sin12xd (sin 2x). в конце концов .j: _ sin4jc. грех 2х. р / _ ~ 16 64 ’48 2) / = $ cos4 x dx. Из уравнения (5)
/ = I ^ (1 -f- COS 2 *) * dx = .1 ^ (1 + 2 cos 2x + cos12лг) dx. Вторичное применение той же формулы дает / = ± 5 (| — + 2soz 2, +++ ^ ++ C № 4. Интеграл \ tffxdx и \ ctg * xdx. интеграл l = \ ig «xdx,
Смотрите также:

