Оглавление:



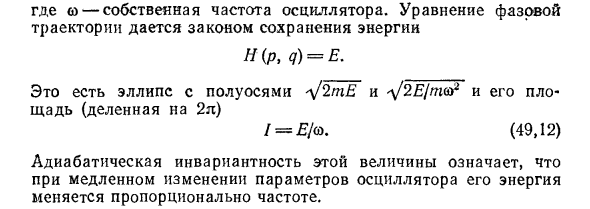

Адиабатические инварианты
- Адиабатический инвариант Рассмотрим механическую систему, которая выполняет одномерное конечное движение и характеризуется определенным параметром A, который определяет саму систему или внешние характеристики. Поле г) где оно находится.
Параметр А есть Внешние причины медленно (как говорится, адиабатические) меняются со временем. Медленный означает изменение, при котором А практически не изменяется в течение периода движения. Т система: T ^ dt 0Xdt ») Правая часть этой формулы Не только от медленно меняющейся переменной A, но и от быстро меняющихся переменных q и p.
В этом случае медленное изменение A Людмила Фирмаль
Чтобы подчеркнуть систематический курс интереса к изменению энергии: Выше мы усредняем равенство (49,2) всего периода путешествия. (и изменение A) позволяет извлечь A из символа усреднения. dE _ dX dN_ ( dt ~ dt <9L ‘^’ А для усредненной функции dN / dL q.
Только р и р рассматриваются как вариации. Это место с постоянным значением L. Явно опишите усреднение дн 1 / дн Ш = г / Вт о Согласно уравнению Гамильтона q = dN / dr дт = дк Дней / др ‘ Используя это уравнение, интеграл по времени заменяется интегралом координат, а период T записывается в виде = / rfi = / e w <49-4) Здесь символ j> указывает интегрирование по полному изменению координат («вперед» и «назад») в период d).
- Таким образом, уравнение (49.3) принимает вид: Гдн / д \ _ dkf dn / dr q hlp дт дт д дк HDN / Dr Как уже упоминалось, интегрирование этого уравнения должно выполняться по некоторой постоянной траектории движения А. Вдоль этой траектории функция Гамильтона имеет постоянное значение E, а импульс является специфической функцией переменной координаты q и двух постоянных независимых параметров E и A.
Понимание импульса Такие функции p (q; E, A) и дифференциалы уравнений H (p, q \ A) = E для параметра A dn, ondr n dn / dh dr F + F d a = 0 или m jr P = -W Подставляя это в верхний интеграл (49.5) и записывая в нижний интеграл в форме dr / dE: _ ГДР _ DE DX? д \ к / (др дэ, д п д \, н ф м * 4 ‘ Это равенство, наконец, можно переписать как 1 = 0, (49,6) /
Результатом является то, что при изменении параметра A Людмила Фирмаль
Указывает на интеграцию (49,7) , т. Е. Является адиабатическим инвариантом. Количество / является функцией энергии системы (и параметров РА А). Его частная производная энергии определяет период Движение: Согласно (49.4) / NI «= t ■ (49,8) или (49,9) Где ω = 2n / T — частота колебаний системы.
Вы можете назначить визуальную геометрию Интегралу (49.7) Другими словами, при использовании понятия фазовой орбиты системы. В этом случае (одна степень свободы) фазовое пространство представляет собой двумерную систему координат p, q и Фазовая траектория системы с периодическим движением является замкнутой кривой в этой плоскости.
Интеграл (49.7), взятый вдоль этой кривой, равен Площадь внутри. Его также можно описать как двумерный интеграл всей области. В качестве примера определим адиабатический инвариант Для одномерного осциллятора.
Его функция Гамильтона Где ω — собственная частота генератора. Уравнение фазовой орбиты задается законом сохранения энергии Эта величина адиабатической инвариантности означает, что когда параметры генератора изменяются медленно, их энергия изменяется пропорционально частоте.
Смотрите также:
| Уравнение Гамильтона-Якоби | Канонические переменные в физике |
| Разделение переменных в физике | Точность сохранения адиабатического инварианта |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

