Оглавление:










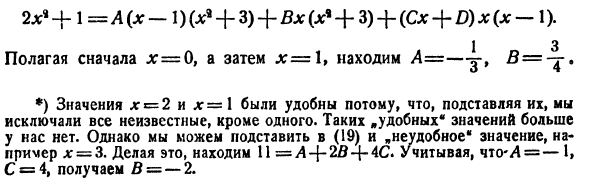

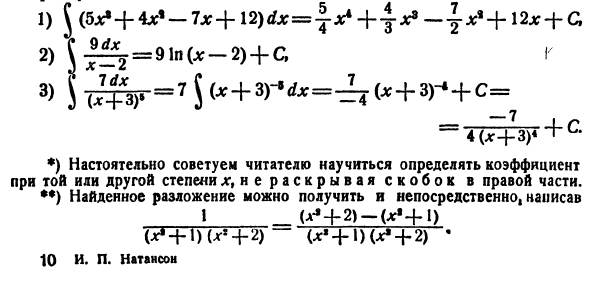

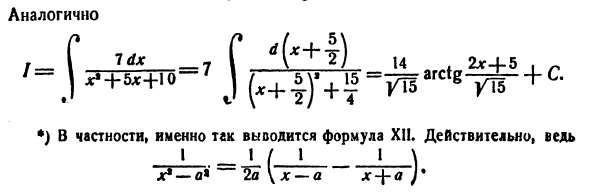

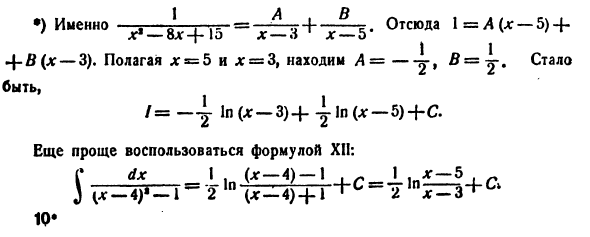

Интегрирование рациональных функций
Рациональная интеграция функций № 1. Постановка вопроса. Обратите внимание, что в конце предыдущего параграфа интеграл элементарной функции не обязательно является самой элементарной функцией. В связи с этим естественно заниматься таким специфическим классом присвоения базовых функций, чтобы интеграция этих функций снова приводила только к базовым функциям. Наиболее важным из этих классов является класс рациональных функций, т. Е.
- Дроби вида В частности, все рациональные полиномы принадлежат этому классу **) a, * + a1 # ++ … + ay. (2) Чтобы объединить дробь (1), они пытаются выразить ее в виде более простой дробной суммы. Так, например, вы можете легко проверить: Юл — 23 _ 3, 7 Откуда s yh — 23 q C dx, n C dx == 3 В (л: -2) + 7 В (л: -3) + С которая разбивает дробь (1) на более простые дроби. Перейдите к этому. n ° 2. Некоторая информация об алгебраических полиномах * Эта n ° описывает свойства алгебраических полиномов вида Axn + Bx «-l +% .. + Px + Qt Все коэффициенты, где A, B и A Q являются действительными числами. Такой полином скоро назовут действительным числом.
Чтобы реализовать эту технику, вам нужно научиться решать чисто алгебраическую задачу, Людмила Фирмаль
Показывает, как эти константы находятся. Этот вопрос иллюстрируется несколькими примерами. 1) Основано на (17) 2x «-ZX + 2 _ A ■ B , _ C ~ (X — I) 1 (x — 2) (x — 1) f * x— \ JC — 2 • 1 Умножьте обе части этого уравнения на знаменатель слева. Это дает нам идентичность 2xr-bx- \ ~ 2 = A (x-2) ~ \ -B (x-1) (g-2) -f-C (je-1) *. (19)
Поскольку уравнение (19) является тождественным, оно также верно для x = 2. Подставляя это значение, 4 = С Следовательно, C = 4. Подставляя x = 1 в (19) 1 = —А Откуда A = -1, поэтому мы смогли найти два коэффициента A и C, используя удобное конкретное значение x *). Эта методика называется «частичное значение * метод». Чтобы найти коэффициент B, используйте другой метод, называемый «Метод сравнения коэффициентов».
Другими словами, коэффициенты x * в левой и правой частях уравнения (19) сделаны равными. 2 = B + C Так что, если мы знаем, что C = 4, B = -2. 2) Разложить на простые дроби 2dga + 1 x (x-l) (* f + 3) ‘ Начните с применения уравнения (17). 2x * — \ — \ _A | B. Cx + P х (х-1) (х «+3) л:> х-1» х ‘+ 3 • Отсюда 2x * + 1 = A (x-1) (* a + 3) +3) + (Cx + -1). 1 3 Предполагая, что сначала x = 0, а затем x = 1, A = -is найдено. *) Значения lg = 2 и lg = 1 были полезны, потому что они заменили их и исключили все, кроме одного неизвестного.
- Больше нет такого «полезного * значения». Однако (19) можно заменить «неудобными» значениями, например, x = z3. Если вы сделаете это, 11 = .D4-2D + 4C. * Если D = -1 и C = 4, то B = -2.
*) Далее сравните jA коэффициенты 0 = A + B + C Итак, C = — Наконец, сравните коэффициенты x. 2 = -A-C-J-D. дать 4 4) Точно так же, применяя (17) 1 _ Ah + B, Cjc + jP (X * + ) (x * + 2) — + 1 «x * + 2 ‘ Отсюда Сравнивая коэффициенты в различных порядках х, x8 X * X 1 O = L + C, о = 2л + а 1 = 2 £ + D. Решение этой системы дает A = C = 0, 5 = 1, D = -1. * ♦), 1 _ 1___1 (Lg + 1) (^ + 2) до x * + \ x * + 2 • № 4.
Интегрирование рациональных чисел. чтобы иметь возможность интегрировать разумную дробь (знаменатель не имеет множественных мнимых корней)? Достаточно понять, что: j x ‘+ px + q- Первые три типа выражений интегрируются без проблем.
Учитывая то, что было сказано при n ° 3, как можно интегрировать четыре типа функций, Людмила Фирмаль
Например 1) J (5 * ”+ 4 *” — 7x + \ 2) dx = \ x> + y ** — y 12 * + G 2) $ 7 = y = »ln (* -2) + GГ -4 (* + 3) ) Читателям настоятельно рекомендуется научиться определять тот или иной фактор x, не открывая правую скобку. ••) Найденную разборку можно получить, написав напрямую. 1 _ + (, + l) U, + 2) — (x ‘+ ) {x> + 2) • 10 и. П. Наттансон
Поэтому мы ориентируемся только на следующие формы интеграции: Кроме того, мы можем предположить, что корень троичного x * — \ — px — \ — q является мнимым. В противном случае эти три члена разлагаются на линейные множители и дроби. Топор + B x ‘+ px + q Он разбивается на простые дроби.
Другими словами, проблема сводится к случаю, который уже рассматривался ). Т.е. известно, что алгебра, это условие мнимого состояния корня троичного х (20 Следовательно, условие (21) считается выполненным. Интеграл (20) легко вычисляется в двух частных случаях. а) Числитель Ax — \ — B является производной от знаменателя x б) Числитель подынтегрального выражения не зависит от x. То есть> 4 = 0. Фактически, в случае а) интеграл (20) является логарифмом знаменателя. Например S ^ -b7 +, e- » ( ‘-b * +1 с) + C S p ^ yzb ^ = 1P ++ 30) + C.
В случае б) интеграл (20) выражается как арктангенс. Для этого выберите полный квадрат из троичного x * — \ — px — \ — q и примените табличное выражение XI. Например , С — 11Сdx-пдикс-А) ) —8lg4-25 ~~) J-4) ~ + 9 ‘ Откуда , А потом. х-4. ^ / = y arctg — ^ — C.
Как хорошо i f_ ™ £ __- 7 G d (X + ~ s) I. 2L- + 5, „ ‘-) ^ M ^ + th-7 J p ^ y ^ = 7EarctgW «+ c- •) В частности, так получается формула XII. Конечно, я 1/1 1 \
Рассмотреть возможность интеграции дх -Vlg + 15 ‘ Если вы попытаетесь применить тот же трюк к 1, -Ох * Dx_ ) (X-4) f-f- (-1) Однако письменный интеграл не соответствует уравнению XI. Это потому, что он не может принять (остается в реальном поле) -1 ea a *. В чем проблема? Дело в том, что реальный корень троичного hch-8jc -f-15 — это jct = 3 и * 9 = 5. Следовательно, интеграл (22) нужно было вычислять иначе *).
В общих чертах, рекомендуемый метод разделения идеальных квадратов состоит в том, что, если корень троичного x * — \ — px — \ — q является мнимым, интегрирование (20 Давайте докажем, что мы можем привести случай б). на самом деле Как упоминалось ранее, мнимый корень троичного выражения гарантирует выполнение неравенства (21), тогда q — и это число равно \ Общий случай интегрирования (20) можно легко свести к случаям a) и b), если числитель Ax — {- B разделить на производную 2lg — \ — p знаменателя x и переписать * * — \ — px — \ — q Используйте Ah — {- B, ID: „Дивиденд равен частному, умноженному на частное плюс остаток *.
Например,•) То есть — = — J. .. = — ^ t-f — ^ — t. Следовательно, 1 = ((:: — 5) + ‘x% -8- + 1o x-хx-5 x’ + -3). Настройки l: = 5 и * = 3, A — j найдено. Быть / = —J 1n (dg-3) 4-1] n (d: ~ 5) + C Упрощает использование XII. D dx_I, (x-4) -1, ^ I 1n * -5 1 квартал
GL V. Неопределенная интеграция Полиномиальный. Свойства многочлена, которые будут интересны позже, сохраняются путем умножения многочлена на постоянный (и ненулевой) коэффициент. Поэтому для простоты используйте самый высокий коэффициент A, A = 1, равный 1. Поэтому вы заинтересованы. Реальный * полином xn + Bxn-l + … + Px + Q (3) Простейшим является полином первого порядка, также называемый линейным.
Форма такого многочлена х-й. (4) 1) Понятно, что корень (единственный) многочлена (4) является вещественным числом a. 2) Полином (4) не может быть учтен *). Следующий комплексный линейный полином (4) представляет собой квадратную тройную функцию **) x * + px + d. (5) Из элементарной алгебры известно, что троичное выражение (5) является факторизованным. + px + q = (x-xi) (x- (6) Где xy и x% — корни трехчлена. Если эти корни действительные, множители x-xx и x- являются полиномами с действительными коэффициентами соответственно.
Если ха является мнимым (то есть это комплексные числа с ненулевыми мнимыми частями), троичное (5) вообще не может быть разложено на реальные факторы. На самом деле, например, три условия l * -8x-f25 (7) Имеют вымышленные корни Когда этот трехчлен раскладывается в действительный линейный полином, он выражается как:
дг-8х + 25 = (х-а) (х-б) •) Речь идет о факторах, которые сами являются полиномами вида (3). Без этой оговорки возможно разложение x-a = -Yx-a x-a = х-а, х-а х — а «_ = -5— • x = -: — • sin x = —-— • и т. Д. Гиацин х е * Факторы вида (3) невозможны, потому что умножение таких факторов добавляет степени.
Следовательно, порядок каждого фактора должен быть меньше, чем порядок продуктов (4). То есть оно должно быть меньше 1. m) Биномиальное выражение x * — * q по-прежнему считается троичным выражением вида (5) с / = 0. (8)
Некоторая информация об алгебраических полиномах Используя действительные числа a и b, эти числа от a до b равны нулю справа, то есть слева от (8), когда они заменяются вместо x. Другими словами, они являются действительными корнями тринома (7), но таких корней нет. Этот вывод может быть выполнен для любого троичного выражения (5) с мнимым корнем.
Таким образом, квадратное троичное выражение (b) либо разлагается на вещественные линейные факторы, либо не разлагается в зависимости от того, является ли его корень действительным или мнимым. При переходе к вещественным кубическим полиномам естественно предсказать, будут ли они разлагаться на реальные факторы более низкого порядка или нет. Однако вы можете видеть, что не существует неразложимого многочлена степени 3. Тоже отлично Все действительные полиномы порядка выше второй теоремы разлагаются на линейные и квадратные коэффициенты.
Эта теорема (доказанная известным немецким математиком Гауссом ) является просто «алгебраической основной теоремой. Следовательно, все полиномы P (x) вида (3) имеют вид P (x) = lx-a) (x-b) (x-c) … ( + px + q) (jfi + rx + s) … 9 (9) Где a, b, c, q, r, s, … являются действительными числами. Числа а, б, c, … являются корнями P (x). Потому что он меняет правую (и, следовательно, левую) часть (9) на 0 (вместо x). Предполагается, что трином x1 — * — px + H 4 «rx + s> •••» τ0 имеет мнимый корень для разложения этих триномов на линейные множители.
Эти корни также являются корнями многочлена P (*). Суммируя эти факторы, P (x) выражается в следующем формате: (10) P (x) = {x-af (x-bf … (x: 1 + px + q) x (g * + hl + s)? …
Здесь уже предполагается, что все факторы разные. Если a = 1, мы говорим, что a — простой маршрут для P (x). Если так Это называется многократным маршрутом P (x). Аналогичные термины используются для мнимого корня из P (x). •) К. Ф. Гаусс (1777–1855). * Даже если бы я сел, чтобы доказать это, все равно не было никакого способа факторизовать полином.
Разница почти одинакова между свидетельством присутствия алюминия на солнце (по крайней мере, спектрографом) и техническим дизайном его доставки.Неопределенный интеграл Пример. если P (x) = (x + 2) (* -1) * (x-b? (X * -8x-f 25) (* «-f I) 4. jc = -2 — простой маршрут для P (x). х = 1-двойной (или двойной) маршрут. х = б-тройной (или тройной) маршрут. Корень троичного x * -8jc +25 (т. Е. Число jrlt, = 4: ± 3 /) — это простой мнимый корень из P (x \ Наконец, троичный корень je ‘+ l (т. Е. Xit f = zt 0 в 4 раза больше корня из P (*). n ° 3. Разложить рациональные дроби на простые дроби.
Рассмотрим разумную часть формата Здесь числитель и знаменатель являются действительными многочленами, то есть многочленами с действительными коэффициентами. При этом условии сама дробь (11) также называется действительным числом. Если порядок числителя меньше порядка знаменателя, дробь называется правильной. Если эти порядки одинаковы или порядок числителя высокий, дробь называется неверной.
Например, из дроби 2x * — \ x «x * + \ Xa-4x + Tl + 2 ‘x * — \ — 2x + b Первое правильно, второе и третье неправильно. При делении нерегулярного дробного числителя на знаменатель (при условии, что оставшаяся дробь, рассматриваемая дробь неприводима), дробь обычно представляется в виде суммы целочисленных полиномов)) доля. Например * -1 1 -2 x * + \ _ g. -x + \ x ‘+ 2 x * + 2’ x * + 2x + b до L x ‘+ 2x + b Поскольку интегрирование целых полиномов выполняется без затруднений (и мы изучаем дробь (11) именно для того, чтобы узнать, как их интегрировать), мы ограничиваем ее нормальными дробями. Чтобы упростить задачу, дробь с несколькими мнимыми корнями в знаменателем.
Допускаются простые корни действительных и мнимых чисел). Проблема интегрирования дробей с множеством мнимых корней в знаменателе обсуждается в более полных учебниках. Так что ищите нормальную реальную дробь **) (Х-а) * (х-б)! … (x * + px + q) (x ‘+ rx + s) …- y’ •) В частности, оно может оказаться постоянным. ••) Предполагается, что ведущий коэффициент знаменателя равен 1. Это потому, что он всегда может быть уменьшен путем деления числителя и знаменателя на этот коэффициент.
Разложить разумные кадры на простые кадры Формат знаменателя предполагает, что дробь (12) может быть получена путем добавления более простой дроби •••••••• …… ••••••• / « (Xo) ** (x-b) P ‘x% + px — \ — q * x’ + hr + 3 •••• {) Числитель этих простых дробей неизвестен, но естественно признать, что дробь (13) также правильна, потому что дробь (12) верна (это можно доказать очень строго).
Таким образом, дробь (12) может быть выражена в следующем формате: Rd (x), Pb (x) Px + o Rx + S, n4v Где Pa (x) t (• )> ••• — неизвестный многочлен, степень которого меньше, чем a, p, … соответственно. Числа P, Q,? И … тоже пока неизвестно. Теперь давайте сосредоточимся на другой части Ра (х) (15) ( — *) • * Поскольку числитель меньше а, его можно записать в следующем виде: = + ^ + + (16) Тем не менее, Ch. Докажите, что все многочлены вида III (§7, n ° 2) (16) могут быть описаны Подстановка этой записи в (15) дает уравнение Rd (x) _ L 1 I I A> -1 (X-s) «(x-a) a» I (x-d-o) * -1 » » ‘x-a 9 Где все молекулы A0, Au … являются своего рода константами. P (x) Подобные выражения возможны для дробей … Сравнивая все вышесказанное, нормальный реальный
Фракция вида (12) разбивается на более простые дроби следующих типов: __ / 00__Ao, A1. ■■ Px + Q. T (17) Здесь молекулы Ar $ Aa_v и числа P, Q, … являются некоторыми константами (пока неизвестными нам!). оставаться
Смотрите также:
| Кривизна | Интегрирование некоторых иррациональностей |
| Общие приемы интегрирования | Интегрирование некоторых трансцендентных функций |

