Оглавление:



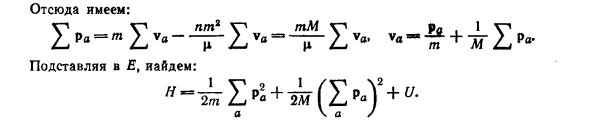

Уравнения Гамильтона в физике
- Уравнение Гамильтона. Формулирование законов механики с использованием функций La Грандж (и уравнения Лагранжа, полученные из него) включает описание механического состояния системы путем установки обобщенных координат и скоростей. Но такое утверждение не Это единственное, что возможно.
Используя обобщенные координаты и импульс системы, мы объясним многие преимущества, особенно при изучении различных общих вопросов по механике. В связи с этим возникает проблема нахождения уравнения движения, соответствующего такой динамической формулировке.
известным в математике как преобразование функции преобразования Лежандра Людмила Фирмаль
Переход от одного набора независимых переменных к другому может быть достигнут преобразованием, . В этом случае это сводится к следующему: Полная производная функции Лагранжа в зависимости от координат и скорости dL = Xr ‘* td4i + Xr-w
В частности, если гамильтонова функция явно не зависит от времени, dH / dt = 0, то есть мы возвращаемся к закону сохранения энергии. С функцией динамических переменных q, q или q, p Лагранж и Гамильтон содержат множество параметров — такими параметрами являются величина A, которая характеризует саму механическую систему или внешнее поле, которое на нее воздействует.
- Если вы думаете об этом как о переменной, Имеет выражение следующей формы вместо (40.1) dL = Y, Pi dqi + EP * dqi + Вместо (40,3) dH = dqi + Y ^ Qi dpi- ^ dX. Найти отношения здесь (Ј) „= — (Ј) * • Ассоциация частных производных по параметру функции A Лагранж и Гамильтон.
Производный индекс Дифференцирование должно быть сделано с константами p и q в одном случае и константами q и q в другом случае. Этот результат можно посмотреть в другом аспекте. Форма функции Лагранжа L = Lo + I /. Где V — небольшое дополнение к основной функции Lo.
Значимость члена с учетом возможности явных зависимостей Лагранж работает вовремя Людмила Фирмаль
Соответствующее сложение функции Гамильтона H = H $ + H ‘ Отношение (H ‘) r, q = — (L%, q- (40-7) При преобразовании из (40.1) в (40.3) .
Потому что последний играется В этом аспекте только роль параметров, которые не имеют отношения к выполняемой трансформации. То же, что формула (40.6) Частные производные по времени L и H связаны соотношением (F L = — (F L- (40-8)
Задание 1. Найти функцию Гамильтона одной материальной точки в декартовых, цилиндрических или сферических координатах. Ответ: декартовы координаты, w, y, z: n = ^ (p l + P y2 + pi) + U (x, y, z) \ Цилиндрические координаты r, (p, z: lp (~ ^ = H2, P%, 2 + ^ + p i) + U (r, V a. Два \ л ^ Таким образом, пт? мм в-л р а = м ^ ва- ^ ва = — ^ ва, P a | 1 Ва-м ЛМ / Ф / Па ‘ Подставляя Е, + ° —
Смотрите также:
| Соприкосновение твердых тел в физике | Функция Рауса в физике |
| Движение в неинерциальной системе отсчета | Скобки Пуассона в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

